-
ĐẠI SỐ VÀ GIẢI TÍCH - SBT TOÁN 11 NÂNG CAO
-
CHƯƠNG 1: HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
-
CHƯƠNG 2: TỔ HỢP VÀ XÁC SUẤT
-
CHƯƠNG 3: DÃY SỐ, CẤP SỐ CỘNG VÀ CẤP SỐ NHÂN
-
CHƯƠNG 4: GIỚI HẠN
- Bài 1: Dãy số có giới hạn 0
- Bài 2: Dãy có giới hạn hữu hạn
- Bài 3: Dãy có giới hạn vô cực
- Bài 4: Định nghĩa và một số định lí về giới hạn của hàm số
- Bài 5. Giới hạn một bên
- Bài 6: Một vài quy tắc tìm giới hạn vô cực
- Bài 7: Các dạng vô định
- Bài 8: Hàm số liên tục
- Ôn tập chương IV - Giới hạn - SBT Toán 11 Nâng cao
-
CHƯƠNG 5: ĐẠO HÀM
-
ÔN TẬP CUỐI NĂM ĐẠI SỐ VÀ GIẢI TÍCH
-
-
HÌNH HỌC-SBT TOÁN 11 NÂNG CAO
-
CHƯƠNG 1: PHÉP DỜI HÌNH VÀ PHÉP ĐỒNG DẠNG
- Bài 1, 2: Mở đầu về phép biến hình. Phép tịnh tiến và phép dời hình
- Bài 3: Phép đối xứng trục
- Bài 4: Phép quay và phép đối xứng tâm
- Bài 5: Hai hình bằng nhau
- Bài 6, 7: Phép vị tự. Phép đồng dạng
- Ôn tập chương 1: Phép dời hình và phép đồng dạng
- Bài tập trắc nghiệm chương 1 - Phép dời hình và phép đồng dạng
-
CHƯƠNG 2: ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG
-
CHƯƠNG 3. VECTƠ KHÔNG GIAN. QUAN HỆ VUÔNG GÓC
- Bài 1. Vectơ trong không gian. Sự đồng phẳng của các vectơ
- Bài 2, 3, 4: Hai đường thẳng vuông góc. Đường thẳng vuông góc với mặt phẳng. Hai mặt phẳng vuông góc
- Bài 5: Khoảng cách
- Ôn tập chương III. Vectơ trong không gian. Quan hệ vuông góc
- Bài tập trắc nghiệm chương III. Vectơ trong không gian. Quan hệ vuông góc.
-
ÔN TẬP CUỐI NĂM - HÌNH HỌC
-
Câu 5.7 trang 179 sách bài tập Đại số và Giải tích 11 Nâng cao
Một viên đạn được bắn lên trời từ một vị trí cách mặt đất 1000m theo phương thẳng đứng với vận tốc ban đầu
Một viên đạn được bắn lên trời từ một vị trí cách mặt đất 1000m theo phương thẳng đứng với vận tốc ban đầu \({v_0} = 245m/s\) (bỏ qua sức cản không khí) .
LG a
Tìm thời điểm \({t_0}\) tại đó viên đạn đạt tốc độ cao nhất và sẽ bắt đầu rơi. Khi đó viên đạn cách mặt đất bao nhiêu mét?
Lời giải chi tiết:
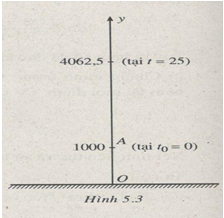
Chọn Oy theo phương thẳng đứng, chiều dương hướng từ mặt đất lên trời, gốc O ở mặt đất và A là vị trí viên đạn được bắn lên, gốc thời gian (từ lúc t = 0) được tính từ vị trí A (h.5.3); khi đó chuyển động của viên đạn là chuyển động biến đổi với vận tốc ban đầu và với gia tốc \(g = - 9,8\,\,m/{s^2}\). (Gia tốc nhận giá trị âm vì vecto gia tốc ngược chiều dương của trục Oy). Phương trình chuyển động của viên đạn là
\(y = 1000 + 245t - 4,9{t^2}\)
Ta có \(v\left( t \right) = y' = 245 - 9,8t\)
Viên đạn đạt độ cao lớn nhất và sẽ bắt đầu rơi khi
\(v\left( t \right) = 0 \Leftrightarrow 245 - 9,8t = 0 \Leftrightarrow t = 25\,\,\left( s \right)\)
Khi đó viên đạn cách mặt đất là
\(y\left( {25} \right) = 1000 + 245.25 - 4,{9.25^2} = 4062,5\,\,\left( m \right)\)
LG b
Sau bao nhiêu giây (kể từ lúc bắn), viên đạn rơi xuống mặt đất?
Lời giải chi tiết:
Viên đạn rơi đến đất khi \(y = 0\). Vậy nếu gọi \({t_1}\) là thời gian kể từ khi viên đạn được bắn lên trời đến khi nó rơi tới đất thì \({t_1}\) phải là nghiệm dương của phương trình.
\(0 = 1000 + 245t - 4,9{t^2} \Leftrightarrow {t_1} = 54\,\,\left( s \right)\)
Loigiaihay.com
Bình luận
Chia sẻ
- Câu 5.6 trang 179 sách bài tập Đại số và Giải tích 11 Nâng cao
- Câu 5.5 trang 179 sách bài tập Đại số và Giải tích 11 Nâng cao
- Câu 5.4 trang 179 sách bài tập Đại số và Giải tích 11 Nâng cao
- Câu 5.3 trang 179 sách bài tập Đại số và Giải tích 11 Nâng cao
- Câu 5.2 trang 178 sách bài tập Đại số và Giải tích 11 Nâng cao
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay
2K7 tham gia ngay group để nhận thông tin thi cử, tài liệu miễn phí, trao đổi học tập nhé!
>> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục
