Bài 7 trang 47 Vở bài tập toán 9 tập 2

Giải bài 7 trang 47 VBT toán 9 tập 2. Biết rằng đường cong trên hình 14 là pararabol y = ax^2...

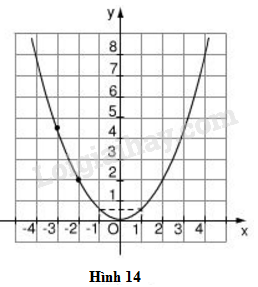
Lựa chọn câu để xem lời giải nhanh hơn

Biết rằng đường cong trên hình 14 là pararabol y = ax²

LG a

Tìm hệ số a

Phương pháp giải:

Thay tọa độ điểm xác định được trên hình vẽ vào hàm số \(y = a{x^2}\) để tìm hệ số \(a.\)

Lời giải chi tiết:

Theo hình 14, điểm đã cho thuộc parabol có tọa độ là \(\left( { - 2;2} \right)\). Tọa độ của điểm này thỏa mãn đẳng thức \(y = a{x^2}\). Do đó, ta có \(a{\left( { - 2} \right)^2} = 2\) hay \(4a = 2\)

Vậy \(a = \dfrac{1}{2}.\)

LG b

Tìm tung độ của điểm M thuộc parabol, biết rằng hoành độ của M là -3

Phương pháp giải:

Thay hoành độ của M vào hàm số tìm được để tìm tung độ

Lời giải chi tiết:

Vì \(a = \dfrac{1}{2}\) nên hàm số đã cho là \(y = \dfrac{1}{2}{x^2}\). Điểm M thuộc đồ thị có hoành độ là \( - 3\) thì tung độ của nó là \(y = \dfrac{1}{2}.{\left( { - 3} \right)^2} = \dfrac{9}{2}\)

LG c

Tìm các điểm thuộc parabol có tung độ bằng 8

Phương pháp giải:

Thay tung độ \(y = 8\) vào hàm số tìm được để tìm hoành độ. Từ đó suy ra các điểm thỏa mãn.

Lời giải chi tiết:

Giả sử điểm \(A\left( {x;8} \right)\) thuộc parabol. Khi đó tọa độ của A thỏa mãn đẳng thức \(y = \dfrac{1}{2}{x^2}.\) Như vậy, \(8=\dfrac{1}{2}x^2\). Do đó, \({x^2} = 16\), suy ra \(\left[ \begin{array}{l}x = - 4\\x = 4\end{array} \right.\)

Vậy các điểm cần tìm là \({A_1}\left( { - 4;8} \right);{A_2}\left( {4;8} \right)\).

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

3.6 trên 5 phiếu

Bài tiếp theo

Bài 8 trang 48 Vở bài tập toán 9 tập 2
Giải Bài 8 trang 48 VBT toán 9 tập 2. Cho hai hàm số y=1/3x^2, y=-x+6. Vẽ đồ thị của các hàm số này trên cùng một mặt phẳng tọa độ...
Bài 6 trang 46 Vở bài tập toán 9 tập 2
Giải Bài 6 trang 46 VBT toán 9 tập 2. Trên mặt phẳng tọa độ, trên hình 13, có một điểm M thuộc đồ thị của hàm số y=ax^2...
Bài 5 trang 45 Vở bài tập toán 9 tập 2
Giải Bài 5 trang 45 VBT toán 9 tập 2. Cho ba hàm số y=1/2 x^2, y=x^2, y=2x^2. Vẽ đồ thị của ba hàm số này trên cùng một mặt phẳng tọa độ ...
Bài 4 trang 44 Vở bài tập toán 9 tập 2
Giải Bài 4 trang 44 VBT toán 9 tập 2. Cho hai hàm số y=3/2x^2 và y=-3/2x^2. Điền vào những ô trống (…) ở các bảng sau rồi vẽ hai đồ thị ...
Phần câu hỏi bài 2 trang 43, 44 Vở bài tập toán 9 tập 2
Giải Phần câu hỏi bài 2 trang 43, 44 VBT toán 9 tập 2. Cho hàm số y=ax^2 (a khác 0). Khoanh tròn vào chữ cái đặt trước câu đúng....