-
ĐẠI SỐ - TOÁN 10 NÂNG CAO
-
CHƯƠNG I. MỆNH ĐỀ - TẬP HỢP
-
CHƯƠNG II. HÀM SỐ BẬC NHẤT VÀ BẬC HAI
-
CHƯƠNG III. PHƯƠNG TRÌNH VÀ HỆ PHƯƠNG TRÌNH
-
CHƯƠNG IV. BẤT PHƯƠNG TRÌNH VÀ HỆ BẤT PHƯƠNG TRÌNH
- Bài 1: Bất đẳng thức và chứng minh bất đẳng thức
- Bài 2: Đại cương về bất phương trình
- Bài 3: Bất phương trình và hệ bất phương trình bậc nhất một ẩn
- Bài 4: Dấu của nhị thức bậc nhất
- Bài 5: Bất phương trình và hệ bất phương trình bậc nhất hai ẩn
- Bài 6: Dấu của tam thức bậc hai
- Bài 7: Bất phương trình bậc hai
- Bài 8: Một số phương trình và bất phương trình quy về bậc hai
- Câu hỏi và bài tập ôn tập chương 4
-
CHƯƠNG V. THỐNG KÊ
-
CHƯƠNG VI. GÓC LƯỢNG GIÁC VÀ CÔNG THỨC LƯỢNG GIÁC
-
ÔN TẬP CUỐI NĂM ĐẠI SỐ - TOÁN 10 NÂNG CAO
-
-
HÌNH HỌC - TOÁN 10 NÂNG CAO
-
CHƯƠNG I. VECTƠ
-
CHƯƠNG II. TÍCH VÔ HƯỚNG CỦA HAI VECTƠ VÀ ỨNG DỤNG
-
CHƯƠNG III. PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG
- Bài 1. Phương trình tổng quát của đường thẳng
- Bài 2. Phương trình tham số của đường thẳng
- Bài 3. Khoảng cách và góc
- Bài 4. Đường tròn
- Bài 5. Đường Elip
- Bài 6. Đường hypebol
- Bài 7. Đường Parabol
- Bài 8. Ba đường cônic
- Ôn tập chương III – Phương pháp tọa độ trong mặt phẳng
- Bài tập trắc nghiệm - Chương III. Phương pháp tọa độ trong mặt phẳng - Toán 10 Nâng cao
-
ÔN TẬP CUỐI NĂM HÌNH HỌC - TOÁN 10 NÂNG CAO
-
Giải toán 10, giải bài tập Toán 10 Nâng cao, đầy đủ đại số giải tích và hình học
Bài 3. Hệ thức lượng trong tam giác
Bài 32 trang 66 SGK Hình học 10 nâng cao
Chứng minh rằng diện tích của một tứ giác bằng nửa tích hai đường chéo và sin của góc hợp bởi hai đường chéo đó.
Đề bài
Chứng minh rằng diện tích của một tứ giác bằng nửa tích hai đường chéo và sin của góc hợp bởi hai đường chéo đó.
Phương pháp giải - Xem chi tiết
- Chia tứ giác ABCD thành 4 tam giác nhỏ để tính diện tích mỗi tam giác đó.
- Cộng các kết quả với nhau suy ra đpcm.
Sử dụng công thức diện tích tam giác \[S = \frac{1}{2}ab\sin C\]
Lời giải chi tiết
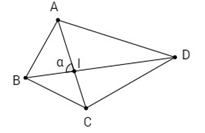
Gọi \(I\) là giao điểm của hai đường chéo \(AC, BD\) và \(\widehat {AIB} = \alpha \).
Ta có \({S_{ABI}} = {1 \over 2}AI.BI.\sin \alpha \)
\({S_{ADI}} = {1 \over 2}AI.DI.\sin ({180^0} - \alpha ) \)
\(= {1 \over 2}AI.DI.\sin \alpha \)
(hai góc bù nhau có sin bằng nhau)
Suy ra \({S_{ABD}} = {S_{ABI}} + {S_{ADI}} \)
\( = \frac{1}{2}AI.BI.\sin \alpha + \frac{1}{2}AI.DI.\sin \alpha \)
\(= {1 \over 2}AI.(BI + DI).\sin \alpha \)
\(= {1 \over 2}AI.BD.\sin \alpha \)
Tương tự ta suy ra:
\({S_{BCD}} = {S_{BIC}} + {S_{CDI}}\)\( = {1 \over 2}CI.BD.\sin \alpha \)
Do đó,
\({S_{ABCD}} = {S_{ABD}} + {S_{BCD}}\)
\( = \frac{1}{2}AI.BD.\sin \alpha + \frac{1}{2}CI.BD.\sin \alpha \)
\(= {1 \over 2}.BD.(AI + CI).\sin \alpha \)
\(= {1 \over 2}.BD.AC.\sin \alpha. \)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 33 trang 66 SGK Hình học 10 nâng cao
- Bài 34 trang 66 SGK Hình học 10 nâng cao
- Bài 35 trang 66 SGK Hình học 10 nâng cao
- Bài 36 trang 66 SGK Hình học 10 nâng cao
- Bài 37 trang 67 SGK Hình học 10 nâng cao
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
