 Giải toán 10, giải bài tập Toán 10 Nâng cao, đầy đủ đại số giải tích và hình học
Giải toán 10, giải bài tập Toán 10 Nâng cao, đầy đủ đại số giải tích và hình học
 Bài 3. Hệ thức lượng trong tam giác
Bài 3. Hệ thức lượng trong tam giác
Bài 25 trang 66 SGK Hình học 10 nâng cao
Tam giác ABC có
Đề bài
Tam giác \(ABC\) có \(a = 5,\,b = 4,\,c = 3\). Lấy điểm \(D\) đối xứng với \(B\) qua \(C\). Tính độ dài \(AD\).
Phương pháp giải - Xem chi tiết
- Tính BD=2BC
- Áp dụng công thức trung tuyến trong tam giác ABD lập phương trình ẩn AD.
- Giải phương trình và kết luận.
Lời giải chi tiết
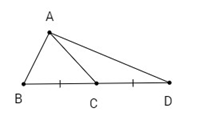
D đối xứng với B qua C nên C là trung điểm BD hay BD=2BC=2.5=10.
Áp dụng công thức tính trung tuyến \(AC\) trong tam giác \(ABD\) ta có
\(A{C^2} = {{A{B^2} + A{D^2}} \over 2} - {{B{D^2}} \over 4}\)
\( \Rightarrow \,\,{4^2} = {{{3^2} + A{D^2}} \over 2} - {{{{10}^2}} \over 4}\)
\( \Leftrightarrow 41 = \frac{{9 + A{D^2}}}{2} \Leftrightarrow 9 + A{D^2} = 82\)
\(\Rightarrow \,A{D^2} = 73\,\,\, \Rightarrow \,AD = \sqrt {73} \approx 8,5.\)
Loigiaihay.com












Danh sách bình luận