Giải toán 10, giải bài tập Toán 10 Nâng cao, đầy đủ đại số giải tích và hình học Bài 3. Hệ thức lượng trong tam giác

Bài 22 trang 65 SGK Hình học 10 nâng cao


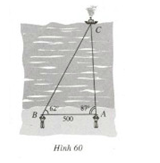
Hình 60 vẽ một chiếc tàu thủy đang neo đậu ở vị trí C trên biển và hai người ở các vị trí quan sát A và B cách nhau 500m.

Đề bài

 Hình 60 vẽ một chiếc tàu thủy đang neo đậu ở vị trí \(C\) trên biển và hai người ở các vị trí quan sát \(A\) và \(B\) cách nhau \(500m\). Họ đo được góc \(CAB\) bằng \({87^0}\) và góc \(CBA\) bằng \({62^0}\).

Tính các khoảng cách \(AC\) và \(BC\).

Phương pháp giải - Xem chi tiết

- Tính C dựa vào công thức A+B+C=180

- Sử dụng định lí sin tính AC, BC:

\(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}}\)

Lời giải chi tiết

Ta có \(\widehat {ACB} = {180^0} - \widehat {BAC} - \widehat {ABC}\) \(= {180^0} - {87^0} - {62^0} = {31^0}\)

Áp dụng định lí sin ta có

\(\begin{array}{l}
\frac{{AB}}{{\sin C}} = \frac{{BC}}{{\sin A}} \Rightarrow \frac{{500}}{{\sin {{31}^0}}} = \frac{{BC}}{{\sin {{87}^0}}}\\
\Rightarrow BC = \frac{{500\sin {{87}^0}}}{{\sin {{31}^0}}} = 969,5\left( m \right)\\
\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}} \Rightarrow \frac{{500}}{{\sin {{31}^0}}} = \frac{{AC}}{{\sin {{62}^0}}}\\
\Rightarrow AC = \frac{{500\sin {{62}^0}}}{{\sin {{31}^0}}} = 857,2\left( m \right)
\end{array}\)

Loigiaihay.com


Bình chọn:
4.2 trên 12 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store