Toán lớp 5, giải toán lớp 5, giải bài tập sgk toán 5 (sách mới)

Lý thuyết tỉ số phần trăm

a) Ví dụ 1: Diện tích một vườn hoa là

Tỉ số phần trăm

\(\dfrac{1}{{100}}\) có thể viết dưới dạng là \(1\% \) , hay \(\dfrac{1}{{100}} = 1\% \) ;

\(\dfrac{{15}}{{100}}\) có thể viết dưới dạng là \(15\% \) , hay \(\dfrac{{15}}{{100}} = 15\% \) ;….

Tổng quát lại \(\dfrac{a}{{100}}\) có thể viết dưới dạng là \(a\% \) , hay \(\dfrac{a}{{100}} = a\% \) ;

\(\% \): Kí hiệu phần trăm.

a) Ví dụ 1: Diện tích một vườn hoa là \(100m^2\), trong đó có \(25m^2\) trồng hoa hồng. Tìm tỉ số của diện tích trồng hoa hồng và diện tích vườn hoa.

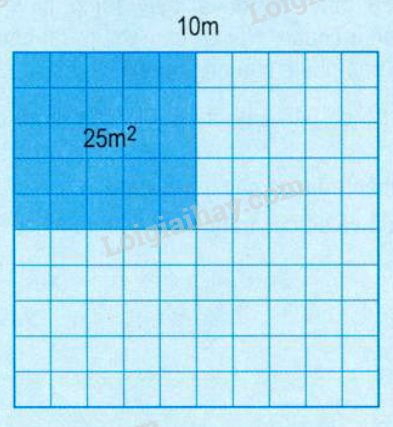
Tỉ số của diện tích trồng hoa hồng và diện tích vườn hoa là \(25 : 100\) hay \(\dfrac{25}{100}\).

Ta viết: \(\dfrac{25}{100}= 25\%\)

Đọc là: hai mươi lăm phần trăm.

Ta nói: Tỉ số phần trăm của diện tích trồng hoa hồng và diện tích vườn hoa hồng là \(25\%\); hoặc: Diện tích trồng hoa hồng chiếm \(25\%\) diện tích vườn hoa.

b) Ví dụ 2: Một trường có \(400\) học sinh, trong đó có \(80\) học sinh giỏi. Tìm tỉ số của số học sinh giỏi và số học sinh toàn trường.

Tỉ số của số học sinh giỏi và số học sinh toàn trường là:

\(80 : 400\) hay \(\dfrac{80}{400}\)

Ta có: \(80 : 400 =\dfrac{80}{400}=\dfrac{20}{100}= 20\%\).

Ta cũng nói rằng: Tỉ số phần trăm của số học sinh giỏi và số học sinh toàn trường là \(20\%\); hoặc: Số học sinh giỏi chiếm \(20\%\) số học sinh toàn trường.

Tỉ số này cho biết cứ \(100\) học sinh của toàn trường thì có \(20\) học sinh giỏi.