Đề kiểm tra 45 phút chương 4 phần Đại số 8 - Đề số 2

Đề bài

Câu 1. (1,5 điểm). Hãy chọn khẳng định đúng. Cho \(c<d\), ta có:

(A) \(c-2>d-2\)

(B) \(-3c<-3d\)

(C) \(3c+2>3d+2\)

(D) \(3c-2<3d-2\)

Câu 2. (1,5 điểm). Hãy chọn khẳng định đúng. Bất phương trình \(7x+14<0\) có tập nghiệm biểu diễn bởi hình vẽ sau:

Câu 3. (2,0 điểm). Giải bất phương trình \(-2x+5>0\) và biểu diễn tập nghiệm trên trục số.

Câu 4. (3,0 điểm). Tìm \(x\) sao cho:

a) Giá trị của biểu thức \(2(x+3)\) nhỏ hơn giá trị của biểu thức \(5-x\).

b) Giá trị của biểu thức \(x-2\) không nhỏ hơn giá trị của biểu thức \(\dfrac{{10 - x}}{3}\).

Câu 5. (2,0 điểm). Giải phương trình \(|-4x|=2x+12\).

Lời giải chi tiết

Câu 1:

Phương pháp:

Sử dụng:

- Khi nhân cả hai vế của một bất đẳng thức với cùng một số âm ta được bất đẳng thức mới ngược chiều với bất đẳng thức đã cho.

- Khi cộng cùng một số vào hai vế của một bất đẳng thức ta được một bất đẳng thức mới cùng chiều với bất đẳng thức đã cho.

Lời giải:

\(\begin{array}{l}
c < d\\
\Leftrightarrow 3c < 3d\\
\Leftrightarrow 3c - 2 < 3d - 2
\end{array}\)

Chọn D.

Câu 2:

Phương pháp:

 - Áp dụng quy tắc chuyển vế và quy tắc nhân với một số khác \(0\) để tìm nghiệm của bất phương trình. Từ đó ta biểu diễn tập nghiệm tìm được trên trục số.

Lời giải:

\(\begin{array}{l}
7x + 14 < 0\\
\Leftrightarrow 7x < - 14\\
\Leftrightarrow x < \left( { - 14} \right):7\\
\Leftrightarrow x < - 2
\end{array}\)

Vậy phương trình có nghiệm là \(x<-2\).

Biểu diễn tập nghiệm của bất phương trình trên trục số như sau:

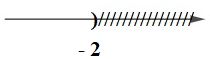
Chọn C.

Phương pháp:

- Áp dụng quy tắc chuyển vế và quy tắc nhân với một số khác \(0\) để tìm nghiệm của bất phương trình. Từ đó ta biểu diễn tập nghiệm tìm được trên trục số.

Lời giải:

\(\begin{array}{l}
- 2x + 5 \ge 0\\
\Leftrightarrow - 2x \ge - 5\\
\Leftrightarrow x \le \dfrac{5}{2}
\end{array}\)

Vậy nghiệm của bất phương trình là \(x \le \dfrac{5}{2}\).

Biểu diễn tập nghiệm trên trục số như sau:

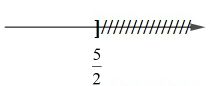
Câu 3:

Phương pháp:

a) Giá trị của biểu thức \(2(x+3)\) nhỏ hơn giá trị của biểu thức \(5-x\) tức là ta giải phương trình \(2\left( {x + 3} \right) < 5 - x\).

b) Giá trị của biểu thức \(x-2\) không nhỏ hơn giá trị của biểu thức \(\dfrac{{10 - x}}{3}\) tức là ta giải phương trình \(x - 2 \ge \dfrac{{10 - x}}{3}\)

Lời giải:

a) Giá trị của biểu thức \(2(x+3)\) nhỏ hơn giá trị của biểu thức \(5-x\) tức là ta giải phương trình \(2\left( {x + 3} \right) < 5 - x\).

\(\begin{array}{l}
2\left( {x + 3} \right) < 5 - x\\
\Leftrightarrow 2x + 6 < 5 - x\\
\Leftrightarrow 2x + x < 5 - 6\\
\Leftrightarrow 3x < - 1\\
\Leftrightarrow x < \dfrac{{ - 1}}{3}
\end{array}\)

Vậy \(x < \dfrac{{ - 1}}{3}\) thì giá trị của biểu thức \(2(x+3)\) nhỏ hơn giá trị của biểu thức \(5-x\).

b) Giá trị của biểu thức \(x-2\) không nhỏ hơn giá trị của biểu thức \(\dfrac{{10 - x}}{3}\) tức là ta giải phương trình \(x - 2 \ge \dfrac{{10 - x}}{3}\).

\(\begin{array}{l}
x - 2 \ge \dfrac{{10 - x}}{3}\\
\Leftrightarrow 3\left( {x - 2} \right) \ge 10 - x\\
\Leftrightarrow 3x - 6 \ge 10 - x\\
\Leftrightarrow 3x + x \ge 10 + 6\\
\Leftrightarrow 4x \ge 16\\
\Leftrightarrow x \ge 4
\end{array}\)

Vậy \(x \ge 4\) thì giá trị của biểu thức \(x-2\) không nhỏ hơn giá trị của biểu thức \(\dfrac{{10 - x}}{3}\).

Câu 4:

Phương pháp:

Các bước giải phương trình chứa dấu giá trị tuyệt đối.

- Bước 1: Áp dụng định nghĩa giá trị tuyệt đối để loại bỏ dấu giá trị tuyệt đôi

- Bước 2: Giải các phương trình không có dấu giá trị tuyệt đối

- Bước 3: Chọn nghiệm thích hợp trong từng trường hợp đang xét

- Bước 4: Kết luận nghiệm.

Lời giải:

\(| - 4x| = -4x\) nếu \(-4x \ge 0\) hay \(x\le 0\).

\(| - 4x| = 4x\) nếu \(-4x<0\) hay \(x>0\).

- Nếu \(x\le 0\) ta có:

\(\begin{array}{l}
- 4x = 2x + 12\\
\Leftrightarrow - 4x - 2x = 12\\
\Leftrightarrow - 6x = 12\\
\Leftrightarrow x = - 2\text{ (t/m)}
\end{array}\)

- Nếu \(x>0\) ta có:

\(\begin{array}{l}
4x = 2x + 12\\
\Leftrightarrow 4x - 2x = 12\\
\Leftrightarrow 2x = 12\\
\Leftrightarrow x = 6\text{ (t/m)}
\end{array}\)

Vậy phương trình đã cho có nghiệm \(x=-2\) và \(x=6\).

Loigiaihay.com