Bài 23 trang 156 Vở bài tập toán 8 tập 1
Giải bài 23 trang 156 vở bài tập toán 8 tập 1. Cho một hình chữ nhật. Vẽ tứ giác có các đỉnh là trung điểm các cạnh của hình chữ nhật...
Đề bài
Cho một hình chữ nhật. Vẽ tứ giác có các đỉnh là trung điểm các cạnh của hình chữ nhật . Vì sao tứ giác này là một hình thoi? So sánh diện tích hình thoi và diện tích hình chữ nhật, từ đó suy ra cách tính diện tích hình thoi.
Phương pháp giải - Xem chi tiết
Sử dụng:
- Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa độ dài cạnh ấy.
- Diện tích hình chữ nhật có kích thước hai cạnh \(a,b\) là \(S=a.b\).
- Diện tích hình thoi bằng nửa tích độ dài hai đường chéo.
\(S=\dfrac{1}{2}{d_1}.{d_2}\)
Lời giải chi tiết
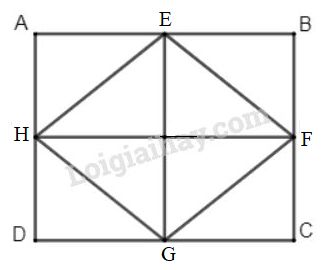
Xét hình chữ nhật \(ABCD\) có \(E, F, G, H\) theo thứ tự là trung điểm của \(AB, BC, CD, DA\).
Ta có \(\Delta AEH = \Delta BEF = \Delta CGF \)\(\,= \Delta DGH\,\,\left( {c.g.c} \right)\)
suy ra \(EH=EF=GF=GH\) nên tứ giác \(EFGH\) là hình thoi.
Ta thấy tám tam giác vuông trong hình bằng nhau nên có diện tích bằng nhau. Hình thoi gồm \(4\) tam giác vuông, hình chữ nhật \(ABCD\) gồm \(8\) tam giác vuông nên diện tích hình thoi bằng \(\dfrac{1}{2}\) diện tích hình chữ nhật.
\({S_{ABCD}} = AD.DC = EG.HF\)
nên \({S_{EFGH}} = \dfrac{1}{2}EG.HF\)
Kết quả trên cho thấy: Diện tích hình thoi bằng nửa tích hai đường chéo.
Loigiaihay.com













Danh sách bình luận