Bài 2.23 trang 61 SBT hình học 12

Giải bài 2.23 trang 61 sách bài tập hình học 12. Cho hình cầu đường kính AA’ = 2r. Gọi H là một điểm trên đoạn AA’ sao cho. Mặt phẳng qua H và vuông góc với AA’ cắt hình cầu theo đường tròn (C).

Đề bài

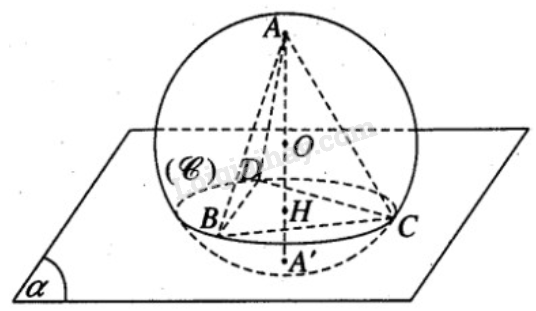
Cho hình cầu đường kính AA’ = 2r. Gọi H là một điểm trên đoạn AA’ sao cho $AH = {{4r} \over 3}$ . Mặt phẳng $(\alpha )$ qua H và vuông góc với AA’ cắt hình cầu theo đường tròn (C).

a) Tính diện tích của hình tròn (C).

b) Gọi BCD là tam giác đều nội tiếp trong (C), hãy tính thể tích hình chóp A.BCD và hình chóp A’.BCD.

Phương pháp giải - Xem chi tiết

a) Công thức tính diện tích hình tròn $S = \pi {R^2}$

b) Thể tích hình chóp: $V = \dfrac{1}{3}Sh$ , ở đó $S$ là diện tích đáy, $h$ là chiều cao.

Lời giải chi tiết

a) Theo giả thiết ta có $\displaystyle AH = {{4r} \over 3}$

Ta suy ra $\displaystyle OH = {r \over 3}$ . Gọi $\displaystyle r’$ là bán kính của đường tròn (C).

Ta có: $\displaystyle r{'^2} = {r^2} - O{H^2}$ $\displaystyle = {r^2} - {{{r^2}} \over 9} = {{8{r^2}} \over 9}$

Vậy diện tích của hình tròn (C) là: $\displaystyle S = \pi r{'^2} = {{8\pi {r^2}} \over 9}$

b) Vì BCD là tam giác đều nên ta có: $\displaystyle BC = r'.\sqrt 3 = {{2\sqrt 6 } \over 3}r$

Diện tích của tam giác đều BCD là $\displaystyle S = {{B{C^2}\sqrt 3 } \over 4} = {{24{r^2}} \over 9}.{{\sqrt 3 } \over 4} = {{2{r^2}\sqrt 3 } \over 3}$

Thể tích hình chóp A.BCD là: $\displaystyle V = {1 \over 3}{{2{r^2}\sqrt 3 } \over 3}.{{4r} \over 3}$ $\displaystyle = {{8\sqrt 3 {r^3}} \over {27}}$

Hai hình chóp A.BCD và A’.BCD có chung mặt đáy BCD nên:

$\displaystyle {{{V_{A'.BCD}}} \over {{V_{A.BCD}}}} = {{HA'} \over {HA}} = {1 \over 2}$ .

Do đó $\displaystyle {V_{A'.BCD}} = {{4\sqrt 3 {r^3}} \over {27}}$ .

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Bài 2.22 trang 61 SBT hình học 12
Giải bài 2.22 trang 61 sách bài tập hình học 12. Cho hình cầu tâm O bán kính r. Lấy một điểm A trên mặt cầu và gọi là mặt phẳng đi qua A sao cho góc giữa OA và bằng 30^0.
Bài 2.21 trang 61 SBT hình học 12
Giải bài 2.21 trang 61 sách bài tập hình học 12. Hình chóp S.ABCD có SA = a là chiều cao của hình chóp và đáy ABCD là hình thang vuông tại A và B có AB = BC = a và AD = 2a. Gọi E là trung điểm của cạnh AD. Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp S.CDE
Bài 2.20 trang 61 SBT hình học 12
Giải bài 2.20 trang 61 sách bài tập hình học 12. Hình tứ diện đều ABCD có cạnh bằng a và có đường cao AH. Gọi O là trung điểm của AH. Xác định tâm và bán kính của mặt cầu ngoại tiếp tứ diện OBCD.
Bài 2.19 trang 61 SBT hình học 12
Giải bài 2.19 trang 61 sách bài tập hình học 12. Chứng minh rằng nếu có một mặt cầu tiếp xúc với 6 cạnh của một hình tứ diện thì hình tứ diện đó có tổng các cặp cạnh đối diện bằng nhau.
Bài 2.18 trang 61 SBT hình học 12
Giải bài 2.18 trang 61 SBT hình học 12. Hình chóp S.ABC là hình chóp tam giác đều , có cạnh đáy bằng a và cạnh bên bằng. Một mặt cầu đi qua đỉnh A và tiếp xúc với hai cạnh SB , SC tại trung điểm của mỗi cạnh.
Bài 2.17 trang 61 SBT hình học 12
Giải bài 2.17 trang 61 sách bài tập hình học 12. Cho mặt cầu tâm O bán kính r. Gọi a là mặt phẳng cách tâm O một khoảng h (0 < h < r) và cắt mặt cầu theo đường tròn (C).
Bài 2.16 trang 60 SBT hình học 12
Giải bài 2.16 trang 60 sách bài tập hình học 12. Cho tứ diện SABC có cạnh SA vuông góc với mặt phẳng (ABC) và có SA = a, AB = b , AC = c. Xác định tâm và bán kính hình cầu ngoại tiếp tứ diện trong các trường hợp sau:
Bài 2.15 trang 60 SBT hình học 12
Giải bài 2.15 trang 60 SBT hình học 12. Xác định tâm O và bán kính r của mặt cầu đi qua 5 điểm A, A’, M, M’, M1. Tính diện tích của mặt cầu tâm O nói trên theo a, x = A’M’
Bài 2.14 trang 60 SBT hình học 12
Giải bài 2.14 trang 60 sách bài tập hình học 12. Hình chóp tam giác S.ABC có SA = SB = SC = a và có chiều cao bằng h. Xác định tâm và bán kính của mặt cầu ngoại tiếp hình chóp. Tính diện tích của mặt cầu đó.
Bài 2.13 trang 60 SBT hình học 12
Giải bài 2.13 trang 60 sách bài tập hình học 12. Trong mặt phẳng cho hình vuông ABCD có cạnh bằng a. Trên đường thẳng Ax vuông góc với ta lấy một điểm S tùy ý, dựng mặt phẳng đi qua A và vuông góc với đường thẳng SC. Mặt phẳng cắt SB, SC, SD lần lượt tại B’, C’, D’.

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay

Báo lỗi - Góp ý

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

>> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD - Click xem ngay) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.