-
GIẢI TÍCH SBT - TOÁN 12
-
HÌNH HỌC SBT - TOÁN 12
Bài 2.17 trang 61 SBT hình học 12
Giải bài 2.17 trang 61 sách bài tập hình học 12. Cho mặt cầu tâm O bán kính r. Gọi a là mặt phẳng cách tâm O một khoảng h (0 < h < r) và cắt mặt cầu theo đường tròn (C).
Đề bài
Cho mặt cầu tâm O bán kính r. Gọi \((\alpha )\) là mặt phẳng cách tâm O một khoảng h (0 < h < r) và cắt mặt cầu theo đường tròn (C). Đường thẳng d đi qua một điểm A cố định trên (C) và vuông góc với mặt phẳng \((\alpha )\) cắt mặt cầu tại một điểm B. Gọi CD là đường kính di động của (C)
a) Chứng minh các tổng AD2 + BC2 và AC2 + BD2 có giá trị không đổi.
b) Với vị trí nào của CD thì diện tích tam giác BCD lớn nhất?
c) Tìm tập hợp các điểm H, hình chiếu của B trên CD khi CD chuyển động trên đường tròn (C).
Phương pháp giải - Xem chi tiết
- Chứng minh \(A{D^2} + B{C^2} = A{C^2} + B{D^2} = 4{R^2}\)
- Viết công thức tính diện tích tam giác BCD và suy ra GTLN.
- Nhận xét: H luôn luôn nhìn đọan thẳng AI dưới một góc vuông, từ đó suy ra quỹ tích.
Lời giải chi tiết
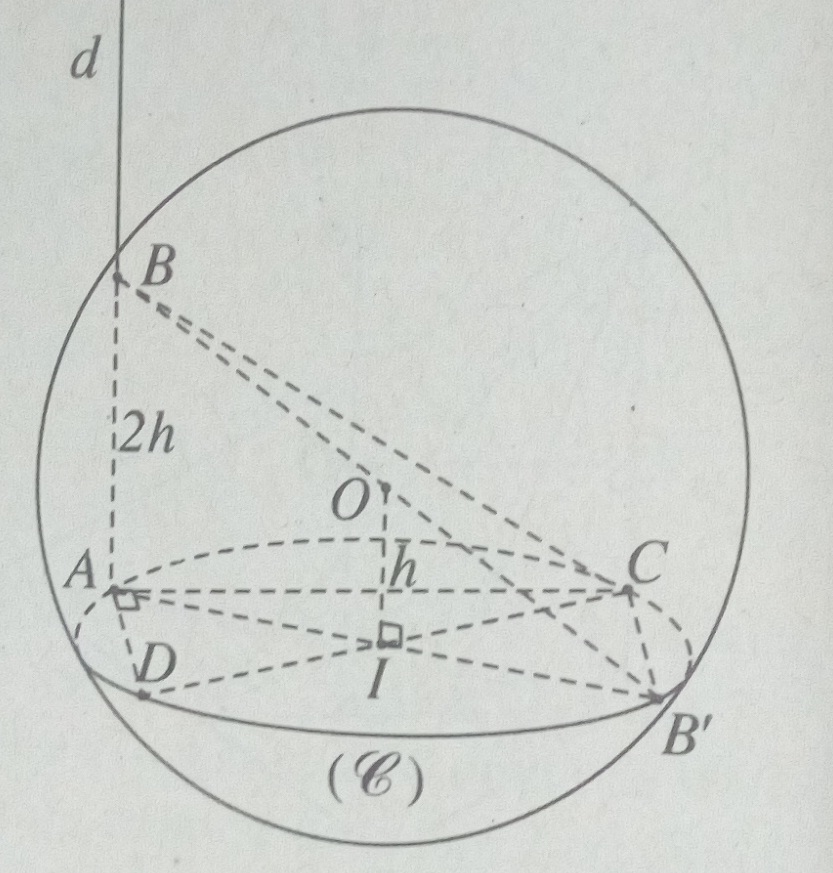
a) Tam giác ADC vuông tại A nên AD2 = DC2 – AC2 (1)
Tam giác ABC vuông tại A nên BC2 = AC2 + AB2 (2)
Từ (1) và (2) ta suy ra AD2 + BC2 = DC2 + AB2 (3)
Ta lại có:
AC2 = DC2 – AD2 và BD2 = AD2 + AB2 (4)
DC2 = 4(r2 – h2) , AB2 = 4h2 (5)
Từ (4) và (5) ta có:
AC2 + BD2 =DC2 + AB2 = 4(r2 – h2) + 4h2 = 4r2 (6)
Từ (3) và (6) ta có: AD2 + BC2 = AC2 + BD2(không đổi)
b) Gọi H là hình chiếu vuông góc của B lên CD.
Diện tích tam giác BCD bằng \({S_{\Delta BCD}} = {1 \over 2}BH.DC\)
Ta thấy, \(BH \le BI\) không đổi nên \({S_{BCD}}\) đạt GTLN khi BH lớn nhất và bằng BI.
Tức là \(BI\bot DC\) \( \Rightarrow DC \bot \left( {ABI} \right) \Rightarrow DC \bot AI\)
Vậy diện tích tam giác BCD lớn nhất khi AI \(\bot\) CD.
c) Ta có
\(\left\{ \begin{array}{l}
AB \bot CD\\
BH \bot CD
\end{array} \right.\) \(\Rightarrow CD \bot \left( {ABH} \right) \Rightarrow CD \bot AH\)
\( \Rightarrow \widehat {AHI} = {90^0}\)
Do đó khi CD di động, điểm H luôn luôn nhìn đọan thẳng AI dưới một góc vuông.
Vậy tập hợp các điểm H là đường tròn đường kính AI nằm trong mặt phẳng \((\alpha )\).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 2.18 trang 61 SBT hình học 12
- Bài 2.19 trang 61 SBT hình học 12
- Bài 2.20 trang 61 SBT hình học 12
- Bài 2.21 trang 61 SBT hình học 12
- Bài 2.22 trang 61 SBT hình học 12
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
