-
PHẦN ĐẠI SỐ - VỞ BÀI TẬP TOÁN 7 TẬP 1
-
CHƯƠNG 1: SỐ HỮU TỈ - SỐ THỰC
- Bài 1. Tập hợp Q các số hữu tỉ
- Bài 2. Cộng, trừ số hữu tỉ
- Bài 3. Nhân, chia số hữu tỉ
- Bài 4. Giá trị tuyệt đối của một số hữu tỉ. Cộng, trừ, nhân, chia số thập phân
- Bài 5. Lũy thừa của một số hữu tỉ
- Bài 6. Lũy thừa của một số hữu tỉ ( tiếp theo)
- Bài 7. Tỉ lệ thức
- Bài 8. Tính chất của dãy tỉ số bằng nhau
- Bài 9. Số thập phân hữu hạn. Số thập phân vô hạn tuần hoàn
- Bài 10. Làm tròn số
- Bài 11. Số vô tỉ. Khái niệm về căn bậc hai
- Bài 12. Số thực
- Ôn tập chương 1 - Số hữu tỉ - Số thực
-
CHƯƠNG 2: HÀM SỐ VÀ ĐỒ THỊ
-
-
PHẦN HÌNH HỌC - VỞ BÀI TẬP TOÁN 7 TẬP 1
-
CHƯƠNG 1: ĐƯỜNG THẲNG VUÔNG GÓC. ĐƯỜNG THẲNG SONG SONG
- Bài 1. Hai góc đối đỉnh
- Bài 2. Hai đường thẳng vuông góc
- Bài 3. Các góc tạo bởi một đường thẳng cắt hai đường thẳng
- Bài 4. Hai đường thẳng song song
- Bài 5. Tiên đề Ơclit về đường thẳng song song
- Bài 6. Từ vuông góc đến song song
- Bài 7. Định lí
- Ôn tập chương 1 - Đường thẳng vuông góc. Đường thẳng song song
-
CHƯƠNG 2: TAM GIÁC
- Bài 1. Tổng ba góc của một tam giác
- Bài 2. Hai tam giác bằng nhau
- Bài 3. Trường hợp bằng nhau thứ nhất của tam giác cạnh - cạnh - cạnh (c.c.c)
- Bài 4. Trường hợp bằng nhau thứ hai của tam giác cạnh - góc - cạnh (c.g.c)
- Bài 5. Trường hợp bằng nhau thứ ba của tam giác góc - cạnh - góc (g.c.g)
- Bài 6. Tam giác cân
- Bài 7. Định lí Py-ta-go
- Bài 8. Các trường hợp bằng nhau của tam giác vuông
- Ôn tập chương 2 - Tam giác
-
-
PHẦN ĐẠI SỐ - VỞ BÀI TẬP TOÁN 7 TẬP 2
-
PHẦN HÌNH HỌC - VỞ BÀI TẬP TOÁN 7 TẬP 2
-
CHƯƠNG 3: QUAN HỆ GIỮA CÁC YẾU TỐ TRONG TAM GIÁC . CÁC ĐƯỜNG ĐỒNG QUY CỦA TAM GIÁC
- Bài 1. Quan hệ giữa góc và cạnh đối diện trong một tam giác
- Bài 2. Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu
- Bài 3. Quan hệ giữa ba cạnh của một tam giác bất đẳng thức tam giác
- Bài 4. Tính chất ba đường trung tuyến của tam giác
- Bài 5. Tính chất tia phân giác của một góc
- Bài 6. Tính chất ba đường phân giác của tam giác
- Bài 7. Tính chất đường trung trực của một đoạn thẳng
- Bài 8. Tính chất ba đường trung trực của tam giác
- Bài 9. Tính chất ba đường cao của tam giác
- Ôn tập chương 3 - Quan hệ giữa các yếu tố trong tam giác. Các đường đồng quy trong tam giác
-
BÀI TẬP ÔN TẬP CUỐI NĂM
-
Bài 16 trang 120 Vở bài tập toán 7 tập 1
Giải bài 16 trang 120 VBT toán 7 tập 1. Trên mỗi hình 25, 26, 27 có các tam giác nào bằng nhau? Vì sao?
Đề bài
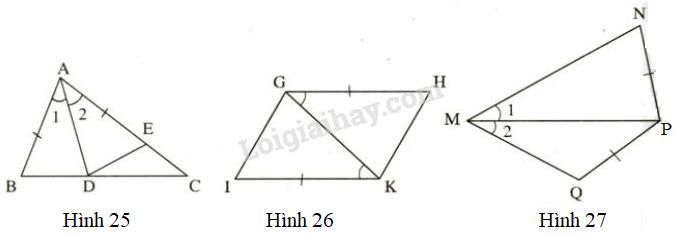
Trên mỗi hình \(25,26,27\) có các tam giác nào bằng nhau? Vì sao?
Phương pháp giải - Xem chi tiết
Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
Lời giải chi tiết
Xét hình 25,
\(∆ADB\) và \(∆ADE\) có: \(AD\) là cạnh chung, \(AB=AE\) (giả thiết), \(\widehat{A_{1}}=\widehat{A_{2}}\) (giả thiết)
Do đó \( ∆ADB = ∆ADE\;(c.g.c)\)
Xét hình 26,
\(∆HGK\) và \(∆IKG\) có: \(GK\) là cạnh chung, \(HG=IK\) (giả thiết), \(\widehat{HGK}=\widehat{IKG}\) (giả thiết)
Do đó \( ∆HGK = ∆IKG( c.g.c)\)
Xét hình 27, không kết luận được hai tam giác nào bằng nhau vì
Xét \(∆PMQ\) và \(∆PMN\) có:
\(MP\) cạnh chung
\(\widehat{M_{1}}=\widehat{M_{2}}\) (giả thiết)
\(PQ=PN\) (giả thiết)
Nhưng \(\widehat{M_{1}}\) không xen giữa hai cạnh \(MP\) và \(PN\)
\(\widehat{M_{2}}\) không xen giữa hai cạnh \(MP\) và \(PQ\)
Nên \(\Delta PMQ\) không bằng \(\Delta PMN\).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 17 trang 121 Vở bài tập toán 7 tập 1
- Bài 18 trang 121 Vở bài tập toán 7 tập 1
- Bài 19 trang 122 Vở bài tập toán 7 tập 1
- Bài 20 trang 122 Vở bài tập toán 7 tập 1
- Bài 21 trang 123 Vở bài tập toán 7 tập 1
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
