Bài 38 trang 93 SGK Đại số và Giải tích 12 Nâng cao
Đơn giản các biểu thức:
Đơn giản các biểu thức:
LG a
\(\log {1 \over 8} + {1 \over 2}\log 4 + 4\log \sqrt 2 \)
Lời giải chi tiết:
\(\log {1 \over 8} + {1 \over 2}\log 4 + 4\log \sqrt 2 \)
\(\begin{array}{l}
= \log \frac{1}{8} + \log {4^{\frac{1}{2}}} + \log {\left( {\sqrt 2 } \right)^4}\\
= \log \frac{1}{8} + \log \sqrt 4 + \log {\left[ {{{\left( {\sqrt 2 } \right)}^2}} \right]^2}\\= \log \frac{1}{8} + \log 2 + \log 4\\
= \log \left( {\frac{1}{8}.2.4} \right)\\
= \log 1\\
= 0
\end{array}\)
LG b
\(\log {4 \over 9} + {1 \over 2}\log 36 + {3 \over 2}\log {9 \over 2}\)
Lời giải chi tiết:
\(\log {4 \over 9} + {1 \over 2}\log 36 + {3 \over 2}\log {9 \over 2}\)
\(\begin{array}{l}
= \log \frac{4}{9} + \log {36^{\frac{1}{2}}} + \log {\left( {\frac{9}{2}} \right)^{\frac{3}{2}}}\\
= \log \frac{4}{9} + \log 6 + \log \left( {\sqrt {{{\left( {\frac{9}{2}} \right)}^3}} } \right)\\
= \log \left( {\frac{4}{9}.6.\sqrt {{{\left( {\frac{9}{2}} \right)}^3}} } \right)\\
= \log \left( {\frac{8}{3}.\frac{9}{2}\sqrt {\frac{9}{2}} } \right)\\
= \log \left( {12.\frac{3}{{\sqrt 2 }}} \right)\\
= \log \left( {18\sqrt 2 } \right)
\end{array}\)
LG c
\(\log 72 - 2\log {{27} \over {256}} + \log \sqrt {108} \)
Lời giải chi tiết:
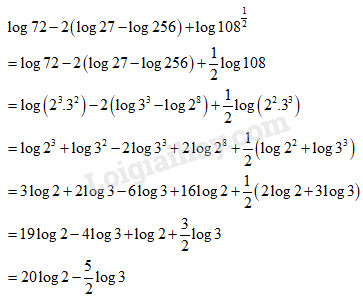
LG d
\(\log {1 \over 8} - \log 0,375 + 2\log \sqrt {0,5625} \)
Lời giải chi tiết:
\(\begin{array}{l}
= \log \frac{1}{8} - \log \frac{3}{8} + \log {\left( {\sqrt {0,5625} } \right)^2}\\
= \log \frac{1}{8} - \log \frac{3}{8} + \log 0,5625\\
= \log \frac{1}{8} - \log \frac{3}{8} + \log \frac{9}{{16}}\\
= \left( {\log \frac{1}{8} + \log \frac{9}{{16}}} \right) - \log \frac{3}{8}\\
= \log \left( {\frac{1}{8}.\frac{9}{{16}}} \right) - \log \frac{3}{8}\\
= \log \frac{9}{{128}} - \log \frac{3}{8}\\
= \log \left( {\frac{9}{{128}}:\frac{3}{8}} \right)\\
= \log \frac{3}{{16}}
\end{array}\)
Loigiaihay.com













Danh sách bình luận