Bài 16 trang 191 SGK Giải tích 12 Nâng cao
Đố vui. Trong mặt phẳng phức cho các điểm: O (gốc tọa độ), A biểu diễn số 1, B biểu diễn số phức z không thực, A' biểu diễn số phức z'...
Đề bài
Đố vui. Trong mặt phẳng phức cho các điểm: O (gốc tọa độ), A biểu diễn số 1, B biểu diễn số phức z không thực, A' biểu diễn số phức \(z'\ne 0\) và B' biểu diễn số phức zz'.
Hai tam giác OAB, OA'B' có phải là hai tam giác dồng dạng không?
Phương pháp giải - Xem chi tiết
Hai tam giác đồng dạng nếu có các cặp cạnh tương ứng tỉ lệ.
Lời giải chi tiết
Do z không phải là số thực nên các điểm O, A, B theo thứ tự biểu diễn các số 0, 1, z là các đỉnh của một tam giác.
Với \(z'\ne 0\), xét các điểm A', B' theo thứ tự biểu diễn các số z', zz' thì ta có:
\({{OA'} \over {OA}} = {{|z'|} \over 1} = |z'|;\) \({{OB'} \over {OB}} = {{|zz'|} \over {|z|}} = |z'|,\) \({{A'B'} \over {AB}} = {{|zz' - z'|} \over {|z - 1|}} = |z'|\)
\(\dfrac{{OA'}}{{OA}} = \dfrac{{OB'}}{{OB}} = \dfrac{{A'B'}}{{AB}} = \left| {z'} \right| \ne 0\)
Vậy tam giác OA'B' đồng dạng với tam giác OAB (tỉ số đồng dạng bằng |z'|).
Cách khác:
Gọi z=a+bi (ab ≠ 0) z'=a'+b' i(a' b' ≠ 0)
Suy ra zz’ = (aa’ – bb’) (a’b +b’a)i
Ta có:
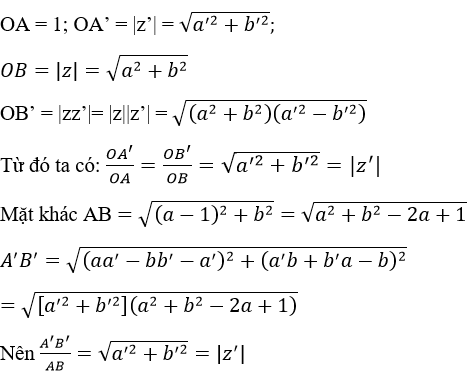
Do đó:
\(\dfrac{{OA'}}{{OA}} = \dfrac{{OB'}}{{OB}} = \dfrac{{A'B'}}{{AB}} = \left| {z'} \right| \ne 0\)
Vậy tam giác OAB đồng dạng với tam giác OA’B’.
Loigiaihay.com













Danh sách bình luận