Bài 1 trang 189 SGK Đại số và Giải tích 12 Nâng cao

Biểu diễn các số đó trong mặt phẳng phức.

Lựa chọn câu để xem lời giải nhanh hơn

Cho các số phức \(2 + 3i; 1 + 2i; 2 – i\)

LG a

Biểu diễn các số đó trong mặt phẳng phức.

Phương pháp giải:

Số phức z=a+bi có điểm biểu diễn M(a;b).

Lời giải chi tiết:

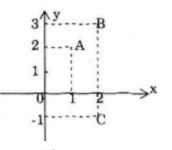
Các điểm A, B, C lần lượt biểu diễn các số phức \(1 + 2i;2 + 3i; 2 – i\)

LG b

Viết số phức liên hợp của mỗi số đó và biểu diễn chúng trong mặt phẳng phức.

Lời giải chi tiết:

Số phức liên hợp của \(2 + 3i\) là: \(2-3i\)

Số phức liên hợp của \(1 + 2i\) là: \(1-2i\)

Số phức liên hợp của \(2 -i\) là: \(2+i\)

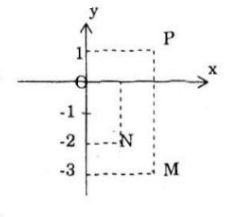
Các điểm M, N, P lần lượt biểu diễn các số phức: \(2-3i\), \(1-2i\), \(2+i\)

LG c

Viết số đối của mỗi số phức đó và biểu diễn chúng trong mặt phẳng phức.

Lời giải chi tiết:

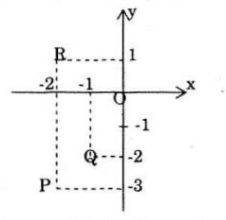
Các số đối của \(2 + 3i; 1 + 2i\) và \(2 – i\) lần lượt là: \(-2 – 3i; -1 – 2i\) và \(-2 + i\) được biểu diễn bởi các điểm: P, Q, R.

Loigiaihay.com

Bình luận

Bình chọn:

3.4 trên 5 phiếu

Bài tiếp theo

Các bài liên quan: - Bài 1. Số phức

Báo lỗi - Góp ý

>> Luyện thi tốt nghiệp THPT và Đại học năm 2021, mọi lúc, mọi nơi tất cả các môn cùng các thầy cô giỏi nổi tiếng, dạy hay dễ hiểu trên Tuyensinh247.com. Đã có đầy đủ các khóa học từ nền tảng tới luyện thi chuyên sâu.