Bài 3 trang 189 SGK Đại số và Giải tích 12 Nâng cao
Xác định các số phức biểu diễn bởi các đỉnh của một lục giác đều có tâm là gốc tọa độ O trong mặt phẳng phức, biết rằng một đỉnh biểu diễn số i.
Đề bài
Xác định các số phức biểu diễn bởi các đỉnh của một lục giác đều có tâm là gốc tọa độ \(O\) trong mặt phẳng phức, biết rằng một đỉnh biểu diễn số i.
Phương pháp giải - Xem chi tiết
Dựng hình suy ra tọa độc các điểm cần tìm.
Lời giải chi tiết
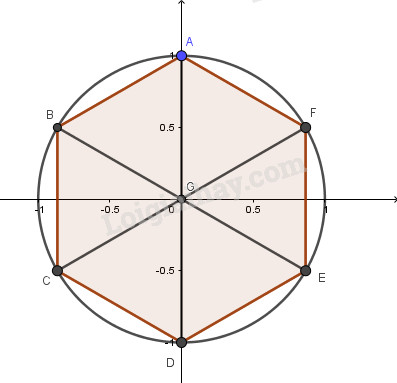
Điểm A(0;1) biểu diễn số \(i\).
F có tọa độ \(\left( {\cos {\pi \over 6};\sin {\pi \over 6}} \right) = \left( {{{\sqrt 3 } \over 2};{1 \over 2}} \right)\).
F biểu diễn số phức \({{\sqrt 3 } \over 2} + {1 \over 2}i.\)
E đối xứng với F qua \(Ox\) nên \(E\left( {\frac{{\sqrt 3 }}{2}; - \frac{1}{2}} \right)\)
E biểu diễn số phức \({{\sqrt 3 } \over 2} - {1 \over 2}i.\)
B đối xứng với E qua O nên \(B\left( {-\frac{{\sqrt 3 }}{2}; \frac{1}{2}} \right)\)
B biểu diễn số \( - {{\sqrt 3 } \over 2} + {1 \over 2}i.\)
C đối xứng với F qua O nên \( C\left( {-{{\sqrt 3 } \over 2};-{1 \over 2}} \right)\)
C biểu diễn số phức \( - {{\sqrt 3 } \over 2} - {1 \over 2}i.\)
D đối xứng với A qua O nên D(0;-1)
D biểu diễn số phức \(–i\).
Loigiaihay.com













Danh sách bình luận