-
GIẢI TÍCH - TOÁN 12 NÂNG CAO
-
CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
- Bài 1. Tính đơn điệu của hàm số
- Bài 2. Cực trị của hàm số
- Bài 3. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
- Bài 4. Đồ thị của hàm số và phép tịnh tiến hệ tọa độ
- Bài 5. Đường tiệm cận của đồ thị hàm số
- Bài 6. Khảo sát sự biến thiên và vẽ đồ thị của một hàm số đa thức
- Bài 7: Khảo sát sự biến thiên và vẽ đồ thị hàm số của một số hàm phân thức hữu tỉ
- Bài 8. Một số bài toán thường gặp về đồ thị
- Câu hỏi và bài tập chương I - Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
- Bài tập trắc nghiệm khách quan chương I - Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số - Toán 12 Nâng cao
-
CHƯƠNG II. HÀM SỐ LŨY THỪA, HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
- Bài 1. Lũy thừa với số mũ hữu tỉ
- Bài 2. Lũy thừa với số mũ thực
- Bài 3. Lôgarit
- Bài 4. Số e và loogarit tự nhiên
- Bài 5. Hàm số mũ và hàm số lôgarit
- Bài 6. Hàm số lũy thừa
- Bài 7. Phương trình mũ và lôgarit
- Bài 8. Hệ phương trình mũ và lôgarit
- Bài 9. Bất phương trình mũ và lôgarit
- Ôn tập chương II - Hàm số lũy thừa, hàm số mũ và hàm số lôgarit
- Bài tập trắc nghiệm khách quan chương II - Hàm số lũy thừa, hàm số mũ và hàm số lôgarit - Toán 12 Nâng cao
-
CHƯƠNG III. NGUYÊN HÀM, TÍCH PHÂN VÀ ỨNG DỤNG
- Bài 1. Nguyên hàm
- Bài 2. Một số phương pháp tìm nguyên hàm
- Bài 3. Tích phân
- Bài 4. Một số phương pháp tích phân
- Bài 5. Ứng dụng tích phân để tính diện tích hình phẳng
- Bài 6. Ứng dụng tích phân để tính thể tích vật thể
- Ôn tập chương III - Nguyên hàm, tích phân và ứng dụng
- Bài tập trắc nghiệm khách quan chương III - Nguyên hàm, tích phân và ứng dụng - Toán 12 Nâng cao
-
CHƯƠNG IV. SỐ PHỨC
-
ÔN TẬP CUỐI NĂM ĐẠI SỐ VÀ GIẢI TÍCH - TOÁN 12 NÂNG CAO
-
-
HÌNH HỌC - TOÁN 12 NÂNG CAO
Giải bài tập Toán 12 Nâng cao, Toán 12 Nâng cao, đầy đủ giải tích và hình học
Ôn tập chương III - Phương pháp tọa độ trong không gian
Bài 10 trang 111 SGK Hình học 12 Nâng cao
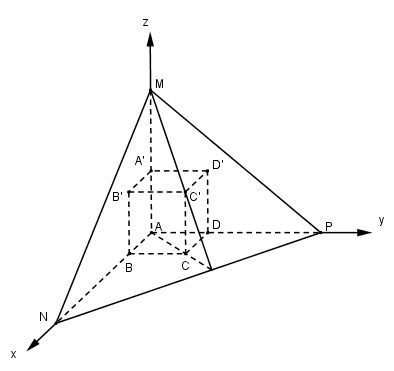
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 1. Trên các tia AA’, AB, AD (có chung gốc A) lần lượt lấy các điểm M, N, P khác A sao cho AM = m, AN = n và AP = p. a) Tìm sự liên hệ giữa m, n và p sao cho mp(MNP) đi qua đỉnh của hình lập phương. b) Trong trường hợp mp(MNP) luôn đi qua C’, hãy tìm thể tích bé nhất của tứ diện AMNP. Khi đó tứ diện AMNP có tính chất gì?
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 1. Trên các tia AA’, AB, AD (có chung gốc A) lần lượt lấy các điểm M, N, P khác A sao cho AM = m, AN = n và AP = p.
LG a
Tìm sự liên hệ giữa m, n và p sao cho mp(MNP) đi qua đỉnh C' của hình lập phương.
Lời giải chi tiết:
Ta chọn Oxyz sao cho O trùng A, các tia Ox, Oy và Oz lần lượt chứa các điểm B, D, A’. Khi đó ta có \(A\left( {0;0;0} \right)\,\,;\,\,B\left( {1;0;0} \right)\,\,;\) \(D\left( {0;1;0} \right)\,\,;\,\,A'\left( {0;0;1} \right)\,;\,\,C'\left( {1;1;1} \right)\,\,;\) \(\,M\left( {0;0;m} \right)\,\,;\,\,N\left( {n;0;0} \right)\,\,;\,\,P\left( {0;p;0} \right)\)
Mặt phẳng (MNP) có phương trình đoạn chắn
\({x \over n} + {y \over p} + {z \over m} = 1\)
Nên mặt phẳng đó đi qua đỉnh C’ khi và chỉ khi:
\({1 \over n} + {1 \over p} + {1 \over m} = 1\,\,\left( * \right)\)
LG b
Trong trường hợp mp(MNP) luôn đi qua C’, hãy tìm thể tích bé nhất của tứ diện AMNP. Khi đó tứ diện AMNP có tính chất gì?
Lời giải chi tiết:
Thể tích tứ diện AMNP là \(V = {1 \over 6}AM.AN.AP = {1 \over 6}mnp\) (trong đó m, n, p là các số dương thỏa mãn điều kiện (*)).
Áp dụng bất đẳng thức Cô-si cho ba số dương, ta có:
\({1 \over n} + {1 \over p} + {1 \over m} \ge 3\root 3 \of {{1 \over {mnp}}} \) \(\Leftrightarrow {1 \over {mnp}} \le {1 \over {{3^3}}} \) \(\Leftrightarrow mnp \ge 27.\)
\( \Rightarrow V = \frac{1}{6}mnp \ge \frac{{27}}{6} = \frac{9}{2}\)
Dấu “=” xảy ra khi và chỉ khi \({1 \over m} = {1 \over n} = {1 \over p} = {1 \over 3}\) \( \Leftrightarrow m = n = p = 3.\)
Vậy giá trị nhỏ nhất của thể tích V là \({{9} \over 2}\), khi đó hình chóp AMNP là hình chóp đều.
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 9 trang 111 SGK Hình học 12 Nâng cao
- Bài 8 trang 111 SGK Hình học 12 Nâng cao
- Bài 7 trang 111 SGK Hình học 12 Nâng cao
- Bài 6 trang 110 SGK Hình học 12 Nâng cao
- Bài 5 trang 110 SGK Hình học 12 Nâng cao
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
