-
Chương 1. Số tự nhiên. Bảng đơn vị đo khối lượng
- Ôn tập các số đến 100000
- Ôn tập các số đến 100000 (tiếp)
- Biểu thức có chứa một chữ
- Các số có sáu chữ số
- Hàng và lớp. So sánh các số có nhiều chữ số
- Triệu và lớp triệu
- Dãy số tự nhiên. Viết số tự nhiên trong hệ thập phân
- So sánh và xếp thứ tự các số tự nhiên
- Yến, tạ, tấn. Bảng đơn vị đo khối lượng
- Giây, thế kỉ
- Tìm số trung bình cộng
- Biểu đồ
- Ôn tập chương 1
-
Chương 2. Bốn phép tính với các số tự nhiên. Hình học
- Phép cộng
- Phép trừ
- Biểu thức có chứa hai chữ, ba chữ
- Tính chất giao hoán của phép cộng
- Tính chất kết hợp của phép cộng
- Tìm hai số khi biết tổng và hiệu của hai số đó
- Góc nhọn, góc tù, góc bẹt
- Hai đường thẳng vuông góc. Hai đường thẳng song song
- Luyện tập chung về phép cộng và phép trừ
- Nhân với số có một chữ số
- Tính chất giao hoán của phép nhân
- Nhân với 10, 100, 1000, … Chia cho 10, 100, 1000, …
- Tính chất kết hợp của phép nhân
- Nhân với số có tận cùng là chữ số 0
- Đề-xi-mét vuông. Mét vuông
- Nhân một số với một tổng
- Nhân một số với một hiệu
- Nhân với số có hai chữ số
- Giới thiệu nhân nhẩm số có hai chữ số với 11
- Nhân với số có ba chữ số
- Luyện tập chung về phép nhân
- Chia một tổng cho một số
- Chia cho số có một chữ số
- Chia một số cho một tích
- Chia một tích cho một số
- Chia hai số có tận cùng là các chữ số 0
- Chia cho số có hai chữ số
- Chia cho số có ba chữ số
- Luyện tập chung về phép chia
- Ôn tập chương 2
-
Chương 3. Dấu hiệu chia hết cho 2 , 5 , 9 , 3. Giới thiệu hình bình hành
-
Chương 4. Phân số - các phép tính với phân số. Hình thoi
- Phân số
- Phân số và phép chia số tự nhiên
- Phân số bằng nhau. Rút gọn phân số
- Quy đồng mẫu số các phân số
- So sánh hai phân số (cơ bản)
- So sánh hai phân số (nâng cao)
- Luyện tập chung về phân số
- Phép cộng phân số
- Phép trừ phân số
- Phép nhân phân số
- Phép chia phân số
- Các bài toán cơ bản về phân số: Tìm giá trị phân số của một số
- Các bài toán cơ bản về phân số: Tìm một số khi biết giá trị phân số của số đó
- Luyện tập chung về các phép tính với phân số
- Hình thoi – Diện tích hình thoi
-
Chương 5. Tỉ số - một số bài toán liên quan đến tỉ số. Tỉ lệ bản đồ
Trắc nghiệm: Phân số bằng nhau. Rút gọn phân số Toán 4
Đề bài
A. Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác \(0\) thì được một phân số bằng phân số đã cho.
B. Nếu cả tử số và mẫu số của một phân số cùng chia hết cho một số tự nhiên khác \(0\) thì sau khi chia ta được một phân số bằng phân số đã cho.
C. Cả A và B đều đúng
D. Cả A và B đều sai
.jpg)
Điền số thích hợp vào ô trống:
Điền số thích hợp vào ô trống:
Trong các phân số sau, phân số nào là phân số tối giản?
A. \(\dfrac{6}{9}\)
B. \(\dfrac{4}{7}\)
C. \(\dfrac{{20}}{{15}}\)
D. \(\dfrac{{15}}{{27}}\)
Trong các phân số dưới đây, phân số nào bằng phân số \(\dfrac{3}{5}\)?
A. \(\dfrac{6}{{15}}\)
B. \(\dfrac{{20}}{{12}}\)
C. \(\dfrac{{15}}{{25}}\)
D. \(\dfrac{{18}}{{36}}\)
Trong các phân số sau, phân số nào bằng với phân số \(\dfrac{4}{7}\)?
\(\dfrac{8}{{14}}\)
\(\dfrac{{16}}{{18}}\)
\(\dfrac{{20}}{{35}}\)
\(\dfrac{{36}}{{63}}\)
\(\dfrac{{100}}{{185}}\)
.jpg)
Rút gọn phân số sau thành phân số tối giản:
\(\dfrac{{4 \times 5 \times 7}}{{7 \times 5 \times 9}} = \dfrac{4}{9}\) . Đúng hay sai?
A. Đúng
B. Sai
Rút gọn phân số \(\dfrac{{72}}{{180}}\) ta được phân số tối giản là:
A. \(\dfrac{2}{5}\)
B. \(\dfrac{3}{5}\)
C. \(\dfrac{{18}}{{45}}\)
D. \(\dfrac{8}{{20}}\)
Rút gọn phân số sau thành phân số tối giản:
Phân số bằng với phân số \(\dfrac{{216}}{{360}}\) và có mẫu số bé nhất là phân số
Tìm số tự nhiên \(a\), biết: \(\dfrac{{20}}{a} = \dfrac{{45}}{{81}}\).
A. \(a = 24\)
B. \(a = 28\)
C. \(a = 36\)
D. \(a = 48\)
Lời giải và đáp án
A. Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác \(0\) thì được một phân số bằng phân số đã cho.
B. Nếu cả tử số và mẫu số của một phân số cùng chia hết cho một số tự nhiên khác \(0\) thì sau khi chia ta được một phân số bằng phân số đã cho.
C. Cả A và B đều đúng
D. Cả A và B đều sai
C. Cả A và B đều đúng
Tính chất cơ bản của phân số:
- Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác \(0\) thì được một phân số bằng phân số đã cho.
- Nếu cả tử số và mẫu số của một phân số cùng chia hết cho một số tự nhiên khác \(0\) thì sau khi chia ta được một phân số bằng phân số đã cho.
Vậy cả A và B đều đúng.
Điền số thích hợp vào ô trống:
Áp dụng tính chất cơ bản của phân số: Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác \(0\) thì được một phân số bằng phân số đã cho.
Ta thấy tử số của phân số \(\dfrac{3}{5}\) nhân với \(2\) thì mẫu số ta cũng nhân với \(2\), khi đó ta được phân số mới bằng phân số \(\dfrac{3}{5}\).
Ta có: \(\dfrac{3}{5} = \dfrac{{3 \times 2}}{{5 \times 2}} = \dfrac{{6\,}}{{10\,}}\).
Điền số thích hợp vào ô trống:
Áp dụng tính chất cơ bản của phân số: Nếu cả tử số và mẫu số của một phân số cùng chia hết cho một số tự nhiên khác \(0\) thì sau khi chia ta được một phân số bằng phân số đã cho.
Ta thấy mẫu số của phân số \(\dfrac{{30}}{{24}}\) chia cho \(6\) thì tử số ta cũng chia cho \(6\), khi đó ta được phân số mới bằng phân số \(\dfrac{{30}}{{24}}\).
Ta có: \(\dfrac{{30}}{{24}} = \dfrac{{30:6}}{{24:6}} = \dfrac{5}{4}\)
Vậy đáp án đúng điền vào chỗ chấm lần lượt từ trái sang phải, từ trên xuống dưới là \(6\,\;,\,5\,;\,\,4\).
Trong các phân số sau, phân số nào là phân số tối giản?
A. \(\dfrac{6}{9}\)
B. \(\dfrac{4}{7}\)
C. \(\dfrac{{20}}{{15}}\)
D. \(\dfrac{{15}}{{27}}\)
B. \(\dfrac{4}{7}\)
- Rút gọn các phân số đã cho (nếu được)
Phân số tối giản là phân số có tử số và mẫu số không cùng chia hết cho một số tự nhiên nào lớn hơn \(1\), hay phân số tối giản là phân số không thể rút gọn được nữa.
Ta có: \(\dfrac{6}{9} = \dfrac{{6:3}}{{9:3}} = \dfrac{2}{3}\,\,\,\, ;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{{20}}{{15}} = \dfrac{{20:5}}{{15:5}} = \dfrac{4}{3}\,\,\, ;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{{15}}{{27}} = \dfrac{{15:3}}{{27:3}} = \dfrac{5}{9}\)
Phân số \(\dfrac{4}{7}\) có tử số và mẫu số không cùng chia hết cho một số tự nhiên nào lớn hơn \(1\), nên \(\dfrac{4}{7}\) là phân số tối giản.
Vậy trong các phân số đã cho, phân số tối giản là phân số \(\dfrac{4}{7}\).
Trong các phân số dưới đây, phân số nào bằng phân số \(\dfrac{3}{5}\)?
A. \(\dfrac{6}{{15}}\)
B. \(\dfrac{{20}}{{12}}\)
C. \(\dfrac{{15}}{{25}}\)
D. \(\dfrac{{18}}{{36}}\)
C. \(\dfrac{{15}}{{25}}\)
Rút gọn các phân số đã cho thành phân số tối giản. Phân số bằng phân số \(\dfrac{3}{5}\) thì rút gọn được về phân số tối giản \(\dfrac{3}{5}\).
Ta có:
\(\dfrac{6}{{15}} = \dfrac{{6:3}}{{15:3}} = \dfrac{2}{5}\,\,\,\,;\,\,\,\,\,\,\ \quad \dfrac{{20}}{{12}} = \dfrac{{20:4}}{{12:4}} = \dfrac{5}{3}\)
\(\dfrac{{15}}{{25}} = \dfrac{{15:5}}{{25:5}} = \dfrac{3}{5}\,\,\,\,;\,\,\,\,\,\, \, \quad \dfrac{{18}}{{36}} = \dfrac{{18:18}}{{36:18}} = \dfrac{1}{2}\)
Vậy trong các phân số đã cho, phân số bằng với phân số \(\dfrac{3}{5}\) là \(\dfrac{{15}}{{25}}\).
Trong các phân số sau, phân số nào bằng với phân số \(\dfrac{4}{7}\)?
\(\dfrac{8}{{14}}\)
\(\dfrac{{16}}{{18}}\)
\(\dfrac{{20}}{{35}}\)
\(\dfrac{{36}}{{63}}\)
\(\dfrac{{100}}{{185}}\)
\(\dfrac{8}{{14}}\)
\(\dfrac{{20}}{{35}}\)
\(\dfrac{{36}}{{63}}\)
Rút gọn các phân số đã cho thành phân số tối giản. Phân số bằng phân số \(\dfrac{4}{7}\) thì rút gọn được về phân số tối giản \(\dfrac{4}{7}\).
Ta có:
\(\begin{array}{l}\dfrac{8}{{14}} = \dfrac{{8:2}}{{14:2}} = \dfrac{4}{7}\,\,\,\,\,\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{{16}}{{18}} = \dfrac{{16:2}}{{18:2}} = \dfrac{8}{9}\,\,\,\,\,\,\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{{20}}{{35}} = \dfrac{{20:5}}{{35:5}} = \dfrac{4}{7};\,\,\,\,\,\,\,\,\,\,\,\,\\\dfrac{{36}}{{63}} = \dfrac{{36:9}}{{63:9}} = \dfrac{4}{7}\,\,\,\,\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{{100}}{{185}} = \dfrac{{100:5}}{{185:5}} = \dfrac{{20}}{{37}} \cdot \,\,\,\,\,\end{array}\)
Vậy các phân số bằng phân số \(\dfrac{4}{7}\) là \(\dfrac{8}{{14}};\,\,\,\,\,\,\,\dfrac{{20}}{{35}};\,\,\,\,\,\,\,\dfrac{{36}}{{63}} \cdot \).
Rút gọn phân số sau thành phân số tối giản:
Ta thấy \(5\) và \(20\) cùng chia hết cho \(5\) nên ta chia cả tử số và mẫu số của phân số \(\dfrac{5}{{20}}\) cho \(5\).
Ta thấy \(5\) và \(20\) cùng chia hết cho \(5\) nên ta có:
\(\dfrac{5}{{20}} = \dfrac{{5:5}}{{20:5}} = \dfrac{1}{4}\)
Vậy đáp án đúng điền vào ô trống lần lượt từ trên xuống dưới là \(1\,;\,\,4\).
\(\dfrac{{4 \times 5 \times 7}}{{7 \times 5 \times 9}} = \dfrac{4}{9}\) . Đúng hay sai?
A. Đúng
B. Sai
A. Đúng
B. Sai
Tích ở tử số và mẫu số đều có thừa số chung là \(5\) và \(7\) nên ta cùng chia nhẩm tích ở tử số và mẫu số cho \(5\), rồi cùng chia nhẩm cho \(7\).
Ta có:
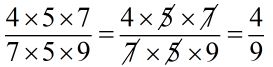
Vậy phép tính đã cho là đúng.
Rút gọn phân số \(\dfrac{{72}}{{180}}\) ta được phân số tối giản là:
A. \(\dfrac{2}{5}\)
B. \(\dfrac{3}{5}\)
C. \(\dfrac{{18}}{{45}}\)
D. \(\dfrac{8}{{20}}\)
A. \(\dfrac{2}{5}\)
Khi rút gọn phân số có thể làm như sau:
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn \(1\).
- Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản.
Ta thấy phân số \(\dfrac{{72}}{{180}}\) có tử số và mẫu số đều chia hết cho \(4\), nên ta có:
\(\dfrac{{72}}{{180}} = \dfrac{{72:4}}{{180:4}} = \dfrac{{18}}{{45}}\)
Ta thấy phân số \(\dfrac{{18}}{{45}}\) có tử số và mẫu số đều chia hết cho \(9\), nên ta có:
\(\dfrac{{18}}{{45}} = \dfrac{{18:9}}{{45:9}} = \dfrac{2}{5}\)
Ta thấy phân số \(\dfrac{2}{5}\) có tử số và mẫu số không cùng chia hết cho số tự nhiên nào lớn hơn \(1\) nên \(\dfrac{2}{5}\) là phân số tối giản.
Vậy \(\dfrac{{72}}{{180}} = \dfrac{2}{5}\).
Rút gọn phân số sau thành phân số tối giản:
Phân tích tử số và mẫu số thành tích của các thừa số, sau đó chia nhẩm tích ở tử số và mẫu số cho các thừa số chung.
Tách \(44\) thành tích của \(11\) và \(4\), tách \(33\) thành tích của \(11\) và \(3\) , tách \(45\) thành tích của \(9\) và \(5\) , ta có:
\(\dfrac{{2 \times 9 \times 44}}{{33 \times 45 \times 7}} = \dfrac{{2 \times 9 \times 11 \times 4}}{{11 \times 3 \times 9 \times 5 \times 7}}\)
Ta thấy tích ở trên gạch ngang và tích ở dưới gạch ngang đều có chung các thừa số là \(9\) và \(11\).
Cùng chia nhẩm tích ở trên gạch ngang và tích ở dưới gạch ngang cho \(9\) và \(11\) ta được:
\(\dfrac{{2 \times 9 \times 44}}{{33 \times 45 \times 7}} = \dfrac{{2 \times 9 \times 11 \times 4}}{{11 \times 3 \times 9 \times 5 \times 7}} = \dfrac{{2 \times 4}}{{3 \times 5 \times 7}} = \dfrac{8}{{105}}\)
Mà \(\dfrac{8}{{105}}\) là phân số tối giản vì có tử số và mẫu số không cùng chia hết cho số tự nhiên nào khác \(1\).
Vậy \(\dfrac{{2 \times 9 \times 44}}{{33 \times 45 \times 7}} = \dfrac{8}{{105}}\)
Đáp án đúng điền vào ô trống lần lượt từ trên xuống dưới là \(8\,;\,\,105\).
Phân số bằng với phân số \(\dfrac{{216}}{{360}}\) và có mẫu số bé nhất là phân số
Phân số bằng với phân số \(\dfrac{{216}}{{360}}\) và có mẫu số bé nhất chính là phân số tối giản sau khi rút gọn phân số \(\dfrac{{216}}{{360}}\).
Phân số cần tìm bằng phân số \(\dfrac{{216}}{{360}}\) và có mẫu số bé nhất chính là phân số tối giản sau khi rút gọn phân số \(\dfrac{{216}}{{360}}\).
Rút gọn phân số \(\dfrac{{216}}{{360}}\) để được phân số tối giản, ta có:
\(\begin{array}{l}\dfrac{{216}}{{360}} = \dfrac{{216:4}}{{360:4}} = \dfrac{{54}}{{90}}\\\dfrac{{54}}{{90}} = \dfrac{{54:9}}{{90:9}} = \dfrac{6}{{10}}\\\dfrac{6}{{10}} = \dfrac{{6:2}}{{10:2}} = \dfrac{3}{5}\end{array}\)
Ta thấy phân số \(\dfrac{3}{5}\) có tử số và mẫu số không cùng chia hết cho số tự nhiên nào lớn hơn \(1\) nên \(\dfrac{3}{5}\) là phân số tối giản.
Do đó, phân số bằng với phân số \(\dfrac{{216}}{{360}}\) và có mẫu số bé nhất là phân số \(\dfrac{3}{5}\).
Vậy đáp án đúng điền vào ô trống lần lượt từ trên xuống dưới là \(3\,;\,\,5\).
Tìm số tự nhiên \(a\), biết: \(\dfrac{{20}}{a} = \dfrac{{45}}{{81}}\).
A. \(a = 24\)
B. \(a = 28\)
C. \(a = 36\)
D. \(a = 48\)
C. \(a = 36\)
Ta có: \(\dfrac{{45}}{{81}} = \dfrac{{45:9}}{{81:9}} = \dfrac{5}{9}\)
Từ đó suy ra: \(\dfrac{{20}}{a} = \dfrac{5}{9}\)
Ta thấy: \(20:5 = 4\).
Do đó, khi nhân cả tử số và mẫu số của phân số \(\dfrac{5}{9}\) với \(4\) ta được phân số mới bằng phân số \(\dfrac{5}{9}\):
\(\dfrac{5}{9} = \dfrac{{5 \times 4}}{{9 \times 4}} = \dfrac{{20}}{{36}}\)
Do đó ta có:
\(\begin{array}{l}\dfrac{{20}}{a} = \dfrac{{20}}{{36}}\\ \Rightarrow a = 36\end{array}\)
Vậy: \(\dfrac{{20}}{{36}} = \dfrac{5}{9} = \dfrac{{45}}{{81}}\).
Đáp án đúng là \(a = 36\).
Luyện tập và củng cố kiến thức Quy đồng mẫu số các phân số Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức So sánh hai phân số Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức So sánh hai phân số (nâng cao) Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Luyện tập chung về phân số Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Phép cộng phân số Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Phép trừ phân số Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Phép nhân phân số Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Phép chia phân số Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các bài toán cơ bản về phân số: Tìm giá trị phân số của một số Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các bài toán cơ bản về phân số: Tìm một số khi biết giá trị phân số của số đó Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Luyện tập chung về các phép tính với phân số Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Hình thoi – Diện tích hình thoi Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Phân số và phép chia số tự nhiên Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Phân số Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
- Trắc nghiệm: Tỉ lệ bản đồ - Ứng dụng của tỉ lệ bản đồ Toán 4
- Trắc nghiệm: Luyện tập chung về tìm hai số khi biết tổng hoặc hiệu và tỉ số của hai số đó Toán 4
- Trắc nghiệm: Tìm hai số khi biết hiệu và tỉ số của hai số đó Toán 4
- Trắc nghiệm: Tìm hai số khi biết tổng và tỉ số của hai số đó Toán 4
- Trắc nghiệm: Giới thiệu tỉ số Toán 4
