-
PHẦN GIẢI TÍCH - TOÁN 12
-
HÌNH HỌC - TOÁN 12
-
Câu hỏi tự luyện Toán 12
-
TẢI 35 ĐỀ KIỂM TRA 15 PHÚT TOÁN 12
-
TẢI 35 ĐỀ KIỂM TRA 1 TIẾT TOÁN 12
-
TẢI 5 ĐỀ THI GIỮA HỌC KÌ 1 TOÁN 12
-
TẢI 20 ĐỀ THI HỌC KÌ 1 TOÁN 12
-
TẢI 6 ĐỀ THI GIỮA HỌC KÌ 2 TOÁN 12
-
TẢI 25 ĐỀ THI HỌC KÌ 2 TOÁN 12
-
TẢI 90 ĐỀ THI THỬ TỐT NGHIỆP THPT
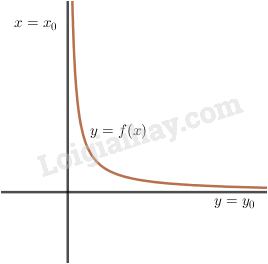
Lý thuyết đường tiệm cận
Cho hàm số y = f(x) có đồ thị (C).
Cho hàm số \(y = f(x)\) có đồ thị \((C)\).
Quảng cáo
1. Tiệm cận đứng
Đường thẳng \(x=a\) là đường tiệm cận đứng của \((C)\) nếu ít nhất một trong bốn điều kiện sau được thoả mãn:
\(\eqalign{
& \mathop {\lim }\limits_{x \to {a^ + }} f(x) = + \infty \cr
& \mathop {\lim }\limits_{x \to {a^ + }} f(x) = - \infty \cr
& \mathop {\lim }\limits_{x \to {a^ - }} f(x) = + \infty \cr
& \mathop {\lim }\limits_{x \to {a^ - }} f(x) = - \infty \cr} \)
2. Tiệm cận ngang
Đường thẳng \(y = b\) là tiệm cận ngang của \((C)\) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
\(\eqalign{
& \mathop {\lim }\limits_{x \to + \infty } f(x) = b \cr
& \mathop {\lim }\limits_{x \to - \infty } f(x) = b \cr} \)
Chú ý
- Đồ thị hàm đa thức không có tiệm cận đứng và tiệm cận ngang, do đó trong các bài toán khảo sát và vẽ đồ thị hàm đa thức, ta không cần tìm các tiệm cận này.
3. Tiệm cận xiên:
Đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) được gọi là tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right)\) nếu nó thỏa mãn một trong 2 điều kiện sau: \(\left[ \begin{array}{l}\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( {ax + b} \right)} \right] = 0\\\mathop {\lim }\limits_{x \to - \infty } \left[ {f\left( x \right) - \left( {ax + b} \right)} \right] = 0\end{array} \right.\) , trong đó:
\(\left\{ \begin{array}{l}a = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{f\left( x \right)}}{x}\\b = \mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - ax} \right]\end{array} \right.\) hoặc \(\left\{ \begin{array}{l}a = \mathop {\lim }\limits_{x \to - \infty } \dfrac{{f\left( x \right)}}{x}\\b = \mathop {\lim }\limits_{x \to - \infty } \left[ {f\left( x \right) - ax} \right]\end{array} \right.\)
Chỉ có khái niệm “Tiệm cận của đồ thị hàm số”, KHÔNG có “Tiệm cận của hàm số”.
Bình luận
Chia sẻ
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
>> Luyện thi TN THPT & ĐH năm 2024 trên trang trực tuyến Tuyensinh247.com. Học mọi lúc, mọi nơi với Thầy Cô giáo giỏi, đầy đủ các khoá: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng; Tổng ôn chọn lọc.
 |
 |
 |
 |
 |
 |
 |
 |
