Phần câu hỏi bài 5 trang 40, 41 Vở bài tập toán 7 tập 2
Giải phần câu hỏi bài 5 trang 40, 41 VBT toán 7 tập 2. Khoanh tròn vào chữ cái trước khẳng định đúng...
Câu 13
Khoanh tròn vào chữ cái trước khẳng định đúng
(A) Bậc của đa thức \(2{x^6} - 3{x^4} - 2{x^6} - 5{x^3} + {x^2} + 2{x^4} \)\(+ x + 3\) là \(6\);
(B) Bậc của đa thức \({x^3}{y^2}{z^4} + \dfrac{2}{3}{x^5}{y^3}{z^4} - \dfrac{3}{4}{x^2}{y^5}{z^2} + {y^2}z\)\( - 4\) là \(12\);
(C) Bậc của đa thức \({x^5}{y^2} + \dfrac{1}{3}{x^2}{y^4}{z^3} + 2\dfrac{3}{4}{x^5}{y^3} + 2x{y^5}{z^4}\)\( - 4xy + x - y + 3\) là \(9\).
Phương pháp giải:
Bậc của đa thức là bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức đó.
Lời giải chi tiết:
Ta có:
\(2{x^6} - 3{x^4} - 2{x^6} - 5{x^3} + {x^2} + 2{x^4} \)\(+ x + 3\)
\( = - {x^4} - 5{x^3} + {x^2} + x + 3\)
Do đó bậc của đa thức \(2{x^6} - 3{x^4} - 2{x^6} - 5{x^3} + {x^2} + 2{x^4} \)\(+ x + 3\) là \(4\).
Bậc của đa thức \({x^3}{y^2}{z^4} + \dfrac{2}{3}{x^5}{y^3}{z^4} - \dfrac{3}{4}{x^2}{y^5}{z^2} + {y^2}z\)\( - 4\) là \(5+3+4=12\).
Bậc của đa thức \({x^5}{y^2} + \dfrac{1}{3}{x^2}{y^4}{z^3} + 2\dfrac{3}{4}{x^5}{y^3} + 2x{y^5}{z^4}\)\( - 4xy + x - y + 3\) là \(1+5+4=10\).
Chọn B.
Câu 14
Điền “\(\times\)” vào ô trống trong bảng sau

Phương pháp giải:
Thay các giá trị của biến đã cho vào đa thức.
Tính giá trị rồi điền dấu \(\times\) vào ô trống thích hợp.
Lời giải chi tiết:
Thay \(x=1,y=-1,z=0\) vào đa thức \({x^5}{y^2} + \dfrac{1}{3}{x^2}{y^4}{z^3} + 2\dfrac{3}{4}{x^5}{y^3} + 2x{y^5}{z^4}\)\(\, - 4xy + x - y + 3\) ta được:
\({1^5}.{\left( { - 1} \right)^2} + \dfrac{1}{3}{.1^2}.{\left( { - 1} \right)^4}.0 \)\(\,+ 2\dfrac{3}{4}{.1^5}.{\left( { - 1} \right)^3} + 2.1.{\left( { - 1} \right)^5}{.0^4}\)\(\, - 4.1.\left( { - 1} \right) + 1 - \left( { - 1} \right) + 3\)
\(= 1 + 0 - \dfrac{{11}}{4} + 0 + 4 + 1 + 1 + 3\)
\(= \dfrac{{29}}{4} = 7\dfrac{1}{4}\)
Thay \(x=-1;y=-2\) vào đa thức \({x^2}y + x{y^5} - 3xy + 2{y^4} - 4{x^3}{y^3}\) ta được:
\({\left( { - 1} \right)^2}.\left( { - 2} \right) + \left( { - 1} \right).{\left( { - 2} \right)^5}\)\(\, - 3.\left( { - 1} \right).\left( { - 2} \right) + 2.{\left( { - 2} \right)^4} \)\(\,- 4.{\left( { - 1} \right)^3}.{\left( { - 2} \right)^3}\)
\(={\left( { - 1} \right)^2}.\left( { - 2} \right) + \left( { - 1} \right).{\left( { - 2} \right)^5} \)\(\,- 3.\left( { - 1} \right).\left( { - 2} \right) + 2.{\left( { - 2} \right)^4} \)\(\,- 4.{\left( { - 1} \right)^3}.{\left( { - 2} \right)^3}\)
\( = - 2 + 32 - 6 + 32 + \left( { - 32} \right) = 24\)
Thay \(x=-1\) vào đa thức \({x^2} - 5{x^3} + {x^6} - 5{x^3} + {x^2} + {x^4} + 2x \)\(\,- 1\) ta được:
\({\left( { - 1} \right)^2} - 5.{\left( { - 1} \right)^3} + {\left( { - 1} \right)^6} - 5.{\left( { - 1} \right)^3} \)\(\,+ {\left( { - 1} \right)^2} + {\left( { - 1} \right)^4} + 2.\left( { - 1} \right) - 1\)
\( = 1 + 5 + 1 + 5 + 1 + 1 - 2 - 1 = 11\)

Câu 15
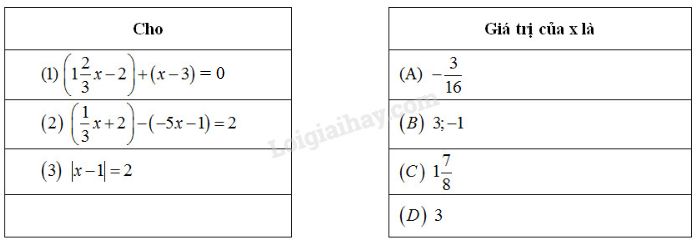
Nối một dòng ở cột bên trái với một dòng ở cột bên phải để được khẳng định đúng
Phương pháp giải:
Chọn giá trị thích hợp của \(x\) để được đẳng thức đúng.
Nối đa thức với giá trị của \(x\) thích hợp.
Lời giải chi tiết:
\(\begin{array}{l}
\left( {1\dfrac{2}{3}x - 2} \right) + \left( {x - 3} \right) = 0\\
\dfrac{5}{3}x - 2 + x - 3 = 0\\
\left( {\dfrac{5}{3} + 1} \right)x = 5\\
\dfrac{8}{3}x = 5\\
x = 5:\dfrac{8}{3}\\
x = \dfrac{{15}}{8} = 1\dfrac{7}{8}
\end{array}\)
\(\begin{array}{l}
\left( {\dfrac{1}{3}x + 2} \right) - \left( { - 5x - 1} \right) = 2\\
\dfrac{1}{3}x + 2 + 5x + 1 = 2\\
\left( {\dfrac{1}{3} + 5} \right)x + 3 = 2\\
\dfrac{{16}}{3}x = 2 - 3\\
\dfrac{{16}}{3}x = - 1\\
x = \left( { - 1} \right):\dfrac{{16}}{3}\\
x = \dfrac{{ - 3}}{{16}}
\end{array}\)
\(|x - 1| = 2\)
\(\Rightarrow x - 1 = 2\) hoặc \(x - 1 = - 2\)
\(x=2+1\) \(x=-2+1\)
\(x=3\) \(x=-1\)
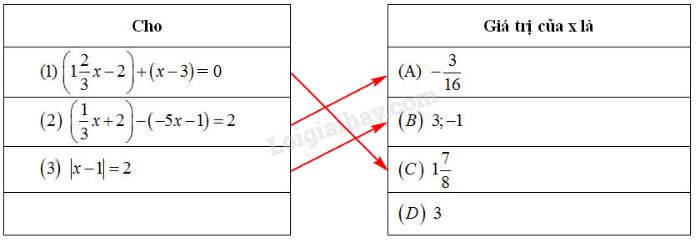
Ta nối như sau:
Loigiaihay.com













Danh sách bình luận