Phần câu hỏi bài 4 trang 36, 37 Vở bài tập toán 7 tập 2

Câu 10.

Nối một biểu thức ở cột bên phải với một biểu thức ở cột bên trái để được hai đơn thức đồng dạng

Phương pháp giải:

- Muốn cộng hoặc trừ các đơn thức đồng dạng, ta cộng hoặc trừ các hệ số với nhau và giữ nguyên phần biến. 

Lời giải chi tiết:

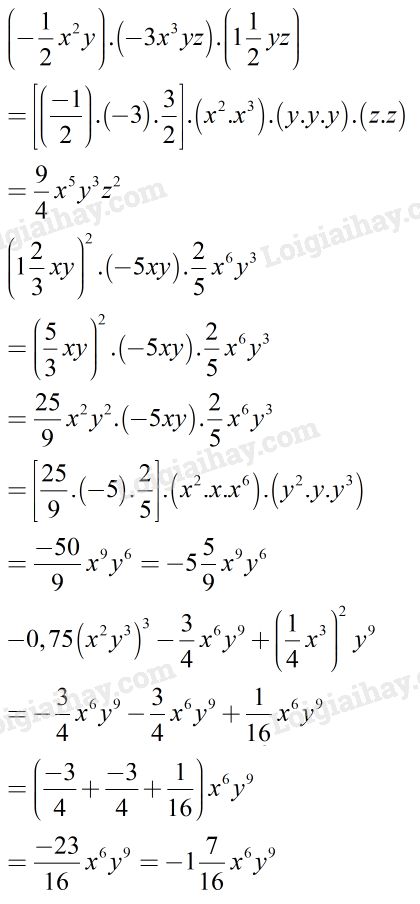
Ta nối như sau: 

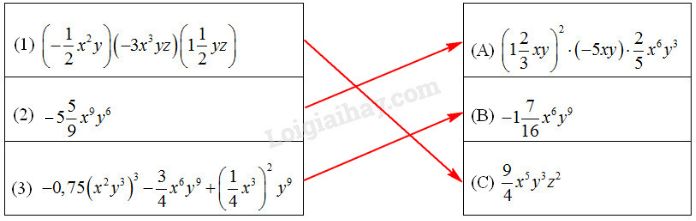
Chú ý: Sửa đề bài \(5\dfrac{5}{9}{x^9}{y^6} \Rightarrow  - 5\dfrac{5}{9}{x^9}{y^6}\) để bài toán có lời giải phù hợp.

Câu 11.

Điền “\(\times\)” vào ô trống trong bảng sau 

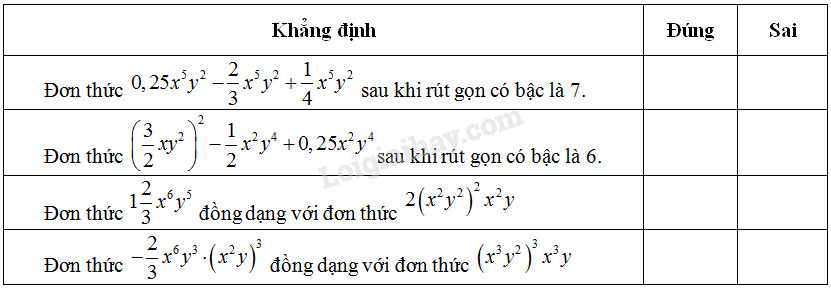
Phương pháp giải:

- Muốn cộng hoặc trừ các đơn thức đồng dạng, ta cộng hoặc trừ các hệ số với nhau và giữ nguyên phần biến.

- Bậc của đơn thức có hệ số khác \(0\) là tổng số mũ của tất cả các biến có trong đơn thức đó. 

Lời giải chi tiết:

Ta điền như sau:

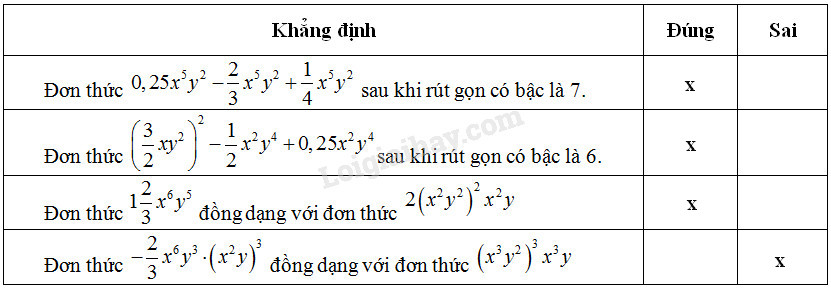
Giải thích: 

\(\begin{array}{l}
0,25{x^5}{y^2} - \dfrac{2}{3}{x^5}{y^2} + \dfrac{1}{4}{x^5}{y^2}\\
= \left( {\dfrac{1}{4} - \dfrac{2}{3} + \dfrac{1}{4}} \right){x^5}{y^2}\\ = \dfrac{{ - 1}}{6}{x^5}{y^2}
\end{array}\)

Đơn thức sau khi rút gọn có bậc là \(7\).

\(\begin{array}{l}
{\left( {\dfrac{3}{2}x{y^2}} \right)^2} - \dfrac{1}{2}{x^2}{y^4} + 0,25{x^2}{y^4}\\
= \dfrac{9}{4}{x^2}{y^4} - \dfrac{1}{2}{x^2}{y^4} + \dfrac{1}{4}{x^2}{y^4}\\
= \left( {\dfrac{9}{4} - \dfrac{1}{2} + \dfrac{1}{4}} \right){x^2}{y^4}\\
= 2{x^2}{y^4}
\end{array}\) 

Đơn thức sau khi rút gọn có bậc là \(6\).

\(2{\left( {{x^2}{y^2}} \right)^2}{x^2}y = 2{x^4}{y^4}.{x^2}y = 2{x^6}{y^5}\)

Do đó đơn thức \(1\dfrac{2}{3}{x^6}{y^5}\) đồng dạng với đơn thức \(2{\left( {{x^2}{y^2}} \right)^2}{x^2}y\)

\(\dfrac{{ - 2}}{3}{x^6}{y^3}{\left( {{x^2}y} \right)^3} = \dfrac{{ - 2}}{3}{x^6}{y^3}.{x^6}{y^3}\)\(\, = \dfrac{{ - 2}}{3}{x^{12}}{y^6}\)

\({\left( {{x^3}{y^2}} \right)^3}{x^3}y = {x^9}{y^6}.{x^3}y = {x^{12}}{y^7}\)

Do đó đơn thức \(\dfrac{{ - 2}}{3}{x^6}{y^3}{\left( {{x^2}y} \right)^3}\) không đồng dạng với \({\left( {{x^3}{y^2}} \right)^3}{x^3}y\).

Câu 12.

Khoanh tròn vào chữ cái trước khẳng định đúng

Hệ số của đơn thức (sau khi rút gọn)

(A) \({x^5}{y^3} - \dfrac{1}{2}{\left( {{x^2}y} \right)^2}xy \)\(\,+ \left( { - \dfrac{2}{3}{x^5}y} \right){\left( { - y} \right)^2}\) là \( - \dfrac{1}{6};\)

(B) \({x^6}{y^3}{z^4} - \dfrac{3}{2}{\left( {{x^3}y{z^2}} \right)^2}y + {\left( { - {x^2}yz} \right)^3}\) là \( - 0,5;\)

(C) \( - \dfrac{2}{5}{\left( {ab} \right)^2}{a^2} - \dfrac{3}{5}ab{\left( {{a^3}b} \right)^3} \)\(\,+ {\left( {1\dfrac{1}{2}{a^2}b} \right)^2}\) là \(1,5;\)

(D) \({\left( { - {a^2}b{c^2}} \right)^3} - \dfrac{3}{5}{\left( { - {a^2}b} \right)^3}{c^6}\) là \(\dfrac{2}{5}\). 

Phương pháp giải:

- Rút gọn đơn thức.

- Tìm hệ số rồi chọn đáp án.

Lời giải chi tiết:

Xét đáp án A:

\({x^5}{y^3} - \dfrac{1}{2}{\left( {{x^2}y} \right)^2}xy \)\(\,+ \left( { - \dfrac{2}{3}{x^5}y} \right){\left( { - y} \right)^2}\)

\( = {x^5}{y^3} - \dfrac{1}{2}{x^5}{y^3} + \left( { - \dfrac{2}{3}} \right){x^5}{y^3}\)

\( = \left( {1 - \dfrac{1}{2} - \dfrac{2}{3}} \right) {x^5}{y^3}= -\dfrac{1}{6}{x^5}{y^3}\)

Đơn thức thu được có hệ số là \(-\dfrac{1}{6}\) nên A đúng. 

Chọn A.

Loigiaihay.com