Phần câu hỏi bài 2 trang 31 Vở bài tập toán 7 tập 2

Câu 4.

Giá trị của biểu thức \(2{x^4}{y^3} + {x^3}{y^2} - xy + {y^3}\) tại \(x = 1; y = -1\) là

(A) \(4;\)                                  (B) \(-1;\)

(C) \(-4;\)                               (D) \(3.\)

Phương pháp giải:

- Thay \(x = 1; y = -1\) vào biểu thức.

- Tính giá trị rồi chọn đáp án thích hợp.

Lời giải chi tiết:

Với \(x = 1; y = -1\) ta được:

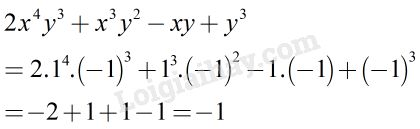
Chọn B.

Câu 5.

Giá trị lớn nhất của biểu thức \(M = 4 - {\left( {x - 2} \right)^2} - \left| {x - 2} \right|\) là

(A) 4;                (B)\(\dfrac{{17}}{4}\);             

(C) 1;                (D) \( - \dfrac{{17}}{4}\).

Phương pháp giải:

- Để \(M\) đạt giá trị lớn nhất (GTLN) thì \({\left( {x - 2} \right)^2} + \left| {x - 2} \right|\) cần đạt giá trị nhỏ nhất (GTNN.) 

Lời giải chi tiết:

Ta có : \(M = 4 - {\left( {x - 2} \right)^2} - \left| {x - 2} \right|\) \( = 4 - \left[ {{{\left( {x - 2} \right)}^2} + \left| {x - 2} \right|} \right]\)

Để M đạt GTLN thì \({\left( {x - 2} \right)^2} + \left| {x - 2} \right|\) đạt GTNN.

Vì \({\left( {x - 2} \right)^2} \ge 0\) với mọi \(x \in R\) và \(\left| {x - 2} \right| \ge 0\) với mọi \( x \in R\) nên GTNN của \({\left( {x - 2} \right)^2} + \left| {x - 2} \right| = 0\) khi \(x = 2\)

Vậy giá trị lớn nhất của biểu thức \(M  = 4\) khi \(x = 2\)

Chọn A.

Câu 6.

Điền "\(\times\)" vào ô trống trong bảng sau

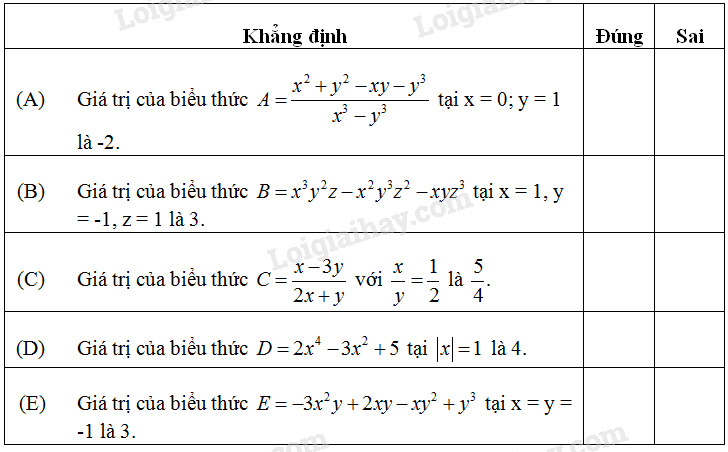
Phương pháp giải:

Muốn tính giá trị của một biểu thức đại số tại những giá trị cho trước của các biến, ta thay các giá trị cho trước đó vào biểu thức rồi thực hiện các phép tính. 

Lời giải chi tiết:

Ta điền như sau: 

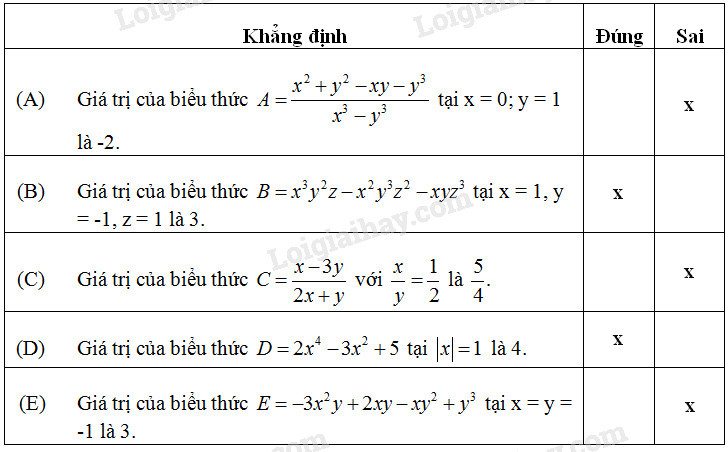
Giải thích:

(A) Thay \(x=0;y=1\) vào biểu thức A ta được:

\(A = \dfrac{{{0^2} + {1^2} - 0.1 - {1^3}}}{{{0^3} - {1^3}}} = \dfrac{0}{{ - 1}} = 0\)

(B) Thay \(x=1;y=-1;z=1\) vào biểu thức B ta được:

\(B = {1^3}.{\left( { - 1} \right)^2}.1 - {1^2}.{\left( { - 1} \right)^3}{.1^2}\)\(\, - 1.\left( { - 1} \right){.1^3} = 1 + 1 + 1 = 3\)

(C) \(\dfrac{x}{y} = \dfrac{1}{2} \Rightarrow x.2 = y.1 \Rightarrow y = 2x\)

Thay \(y=2x\) vào biểu thức C ta được:

\(C = \dfrac{{x - 3.2x}}{{2x + 2x}} = \dfrac{{x - 6x}}{{4x}} = \dfrac{{ - 5x}}{{4x}}\)\(\, = \dfrac{{ - 5}}{4}\)

(D) Ta có:

\(\begin{array}{l}
{x^2} = {\left( {|x|} \right)^2} = {1^2} = 1\\
{x^4} = {\left( {|x|} \right)^4} = {1^4} = 1
\end{array}\)

\( \Rightarrow D = {2.1^4} - {3.1^2} + 5 = 2 - 3 + 5\)\(\, = 4\)

(E) Thay \(x=y=-1\) vào biểu thức E ta được:

\(E =  - 3.{\left( { - 1} \right)^2}.\left( { - 1} \right) + 2.\left( { - 1} \right).\left( { - 1} \right) \)\(\,- \left( { - 1} \right).{\left( { - 1} \right)^2} + {\left( { - 1} \right)^3}\)\(\, = 3 + 2 + 1 - 1 = 5\) 

Loigiaihay.com