-
PHẦN ĐẠI SỐ - VỞ BÀI TẬP TOÁN 8 TẬP 1
-
CHƯƠNG 1: PHÉP NHÂN VÀ CHIA CÁC ĐA THỨC
- Bài 1. Nhân đơn thức với đa thức
- Bài 2. Nhân đa thức với đa thức
- Bài 3. Những hằng đẳng thức đáng nhớ
- Bài 4. Những hằng đẳng thức đáng nhớ (tiếp)
- Bài 5. Những hằng đẳng thức đáng nhớ (tiếp)
- Bài 6. Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
- Bài 7. Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
- Bài 8. Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử
- Bài 9. Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp
- Bài 10. Chia đơn thức cho đơn thức
- Bài 11. Chia đa thức cho đơn thức
- Bài 12. Chia đa thức một biến đã sắp xếp
- Ôn tập chương 1 - Phép nhân và chia các đa thức
-
CHƯƠNG 2: PHÂN THỨC ĐẠI SỐ
- Bài 1. Phân thức đại số
- Bài 2. Tính chất cơ bản của phân thức
- Bài 3. Rút gọn phân thức
- Bài 4. Quy đồng mẫu thức nhiều phân thức
- Bài 5. Phép cộng các phân thức đại số
- Bài 6. Phép trừ các phân thức đại số
- Bài 7. Phép nhân các phân thức đại số
- Bài 8. Phép chia các phân thức đại số
- Bài 9. Biến đổi các biểu thức hữu tỉ. Giá trị của phân thức
- Ôn tập chương 2 - Phân thức đại số
-
-
PHẦN HÌNH HỌC - VỞ BÀI TẬP TOÁN 8 TẬP 1
-
CHƯƠNG 1: TỨ GIÁC
- Bài 1. Tứ giác
- Bài 2. Hình thang
- Bài 3. Hình thang cân
- Bài 4. Đường trung bình của tam giác, của hình thang
- Bài 5. Dựng hình bằng thước và compa. Dựng hình thang
- Bài 6. Đối xứng trục
- Bài 7. Hình bình hành
- Bài 8. Đối xứng tâm
- Bài 9. Hình chữ nhật
- Bài 10. Đường thẳng song song với một đường thẳng cho trước
- Bài 11. Hình thoi
- Bài 12. Hình vuông
- Ôn tập chương 1 - Tứ giác
-
CHƯƠNG 2: ĐA GIÁC - DIỆN TÍCH ĐA GIÁC
-
-
PHẦN ĐẠI SỐ - VỞ BÀI TẬP TOÁN 8 TẬP 2
-
PHẦN HÌNH HỌC - VỞ BÀI TẬP TOÁN 8 TẬP 2
-
CHƯƠNG 3: TAM GIÁC ĐỒNG DẠNG
- Bài 1. Định lí Ta - lét trong tam giác
- Bài 2. Định lí đảo và hệ quả của định lí Ta - lét
- Bài 3. Tính chất đường phân giác của tam giác
- Bài 4. Khái niệm hai tam giác đồng dạng
- Bài 5. Trường hợp đồng dạng thứ nhất (c.c.c)
- Bài 6. Trường hợp đồng dạng thứ hai (c.g.c)
- Bài 7. Trường hợp đồng dạng thứ ba (g.g)
- Bài 8. Các trường hợp đồng dạng của tam giác vuông
- Bài 9. Ứng dụng thực tế của tam giác đồng dạng
- Ôn tập chương 3 - Tam giác đồng dạng
-
CHƯƠNG 4: HÌNH LĂNG TRỤ ĐỨNG. HÌNH CHÓP ĐỀU
- Bài 1. Hình hộp chữ nhật
- Bài 2. Hình hộp chữ nhật (tiếp)
- Bài 3. Thể tích của hình hộp chữ nhật
- Bài 4. Hình lăng trụ đứng
- Bài 5. Diện tích xung quanh của hình lăng trụ đứng
- Bài 6. Thể tích của hình lăng trụ đứng
- Bài 7. Hình chóp đều và hình chóp cụt đều
- Bài 8. Diện tích xung quanh của hình chóp đều
- Bài 9. Thể tích của hình chóp đều
- Ôn tập chương 4 - Hình lăng trụ đứng, hình chóp đều
-
BÀI TẬP ÔN TẬP CUỐI NĂM
-
Bài 6 trang 96 Vở bài tập toán 8 tập 1
Giải bài 6 trang 96 VBT toán 8 tập 1. Tứ giác ABCD có AB= BC và AC tia phân giác của góc A. Chứng minh rằng ABCD là hình thang.
Đề bài
Tứ giác \(ABCD\) có \(AB= BC\) và \(AC\) tia phân giác của góc \(A\). Chứng minh rằng \(ABCD\) là hình thang.
Phương pháp giải - Xem chi tiết
Áp dụng:
- Dấu hiệu nhận biết hình thang: Hình thang là tứ giác có hai cạnh đối song song.
- Chứng minh hai đường thẳng song song ta chứng minh cặp góc so le trong bằng nhau.
Lời giải chi tiết
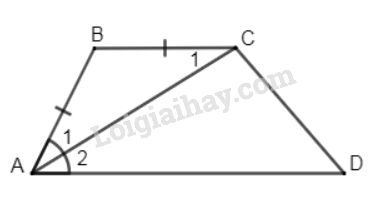
Tam giác \(ABC\) có \(AB = BC\) nên \(∆ABC\) cân tại \(B\), suy ra \(\widehat{A_{1}}=\widehat{BCA}\) (1)
\(AC\) là phân giác của \(\widehat{A}\) nên suy ra \(\widehat{A_{1}}= \widehat{A_{2}}\) (2)
Từ (1) và (2) suy ra \(\widehat{BCA}=\widehat{A_{2}},\) do đó \(BC // AD\) (vì \(\widehat{BCA}\) và \(\widehat{A_{2}}\) so le trong )
Vậy \(ABCD\) là hình thang (dấu hiệu nhận biết hình thang).
Loigiaihay.com
Bình luận
Chia sẻ
Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay
Tham Gia Group Dành Cho Lớp 8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
