-
PHẦN ĐẠI SỐ - VỞ BÀI TẬP TOÁN 7 TẬP 1
-
CHƯƠNG 1: SỐ HỮU TỈ - SỐ THỰC
- Bài 1. Tập hợp Q các số hữu tỉ
- Bài 2. Cộng, trừ số hữu tỉ
- Bài 3. Nhân, chia số hữu tỉ
- Bài 4. Giá trị tuyệt đối của một số hữu tỉ. Cộng, trừ, nhân, chia số thập phân
- Bài 5. Lũy thừa của một số hữu tỉ
- Bài 6. Lũy thừa của một số hữu tỉ ( tiếp theo)
- Bài 7. Tỉ lệ thức
- Bài 8. Tính chất của dãy tỉ số bằng nhau
- Bài 9. Số thập phân hữu hạn. Số thập phân vô hạn tuần hoàn
- Bài 10. Làm tròn số
- Bài 11. Số vô tỉ. Khái niệm về căn bậc hai
- Bài 12. Số thực
- Ôn tập chương 1 - Số hữu tỉ - Số thực
-
CHƯƠNG 2: HÀM SỐ VÀ ĐỒ THỊ
-
-
PHẦN HÌNH HỌC - VỞ BÀI TẬP TOÁN 7 TẬP 1
-
CHƯƠNG 1: ĐƯỜNG THẲNG VUÔNG GÓC. ĐƯỜNG THẲNG SONG SONG
- Bài 1. Hai góc đối đỉnh
- Bài 2. Hai đường thẳng vuông góc
- Bài 3. Các góc tạo bởi một đường thẳng cắt hai đường thẳng
- Bài 4. Hai đường thẳng song song
- Bài 5. Tiên đề Ơclit về đường thẳng song song
- Bài 6. Từ vuông góc đến song song
- Bài 7. Định lí
- Ôn tập chương 1 - Đường thẳng vuông góc. Đường thẳng song song
-
CHƯƠNG 2: TAM GIÁC
- Bài 1. Tổng ba góc của một tam giác
- Bài 2. Hai tam giác bằng nhau
- Bài 3. Trường hợp bằng nhau thứ nhất của tam giác cạnh - cạnh - cạnh (c.c.c)
- Bài 4. Trường hợp bằng nhau thứ hai của tam giác cạnh - góc - cạnh (c.g.c)
- Bài 5. Trường hợp bằng nhau thứ ba của tam giác góc - cạnh - góc (g.c.g)
- Bài 6. Tam giác cân
- Bài 7. Định lí Py-ta-go
- Bài 8. Các trường hợp bằng nhau của tam giác vuông
- Ôn tập chương 2 - Tam giác
-
-
PHẦN ĐẠI SỐ - VỞ BÀI TẬP TOÁN 7 TẬP 2
-
PHẦN HÌNH HỌC - VỞ BÀI TẬP TOÁN 7 TẬP 2
-
CHƯƠNG 3: QUAN HỆ GIỮA CÁC YẾU TỐ TRONG TAM GIÁC . CÁC ĐƯỜNG ĐỒNG QUY CỦA TAM GIÁC
- Bài 1. Quan hệ giữa góc và cạnh đối diện trong một tam giác
- Bài 2. Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu
- Bài 3. Quan hệ giữa ba cạnh của một tam giác bất đẳng thức tam giác
- Bài 4. Tính chất ba đường trung tuyến của tam giác
- Bài 5. Tính chất tia phân giác của một góc
- Bài 6. Tính chất ba đường phân giác của tam giác
- Bài 7. Tính chất đường trung trực của một đoạn thẳng
- Bài 8. Tính chất ba đường trung trực của tam giác
- Bài 9. Tính chất ba đường cao của tam giác
- Ôn tập chương 3 - Quan hệ giữa các yếu tố trong tam giác. Các đường đồng quy trong tam giác
-
BÀI TẬP ÔN TẬP CUỐI NĂM
-
Bài 52 trang 95 Vở bài tập toán 7 tập 2
Giải bài 52 trang 95, 96 VBT toán 7 tập 2. Áp dụng bài 51, chứng minh rằng : Tâm đường tròn ngoại tiếp một tam giác vuông là trung điểm cạnh huyền của tam giác đó. Từ đó, ...
Đề bài
Áp dụng bài 51, chứng minh rằng: Tâm đường tròn ngoại tiếp một tam giác vuông là trung điểm cạnh huyền của tam giác đó. Từ đó, hãy tính độ dài đường trung tuyến xuất phát từ đỉnh góc vuông theo độ dài cạnh huyền của một tam giác vuông.
Phương pháp giải - Xem chi tiết
Sử dụng bài 51.
Chứng minh \(O\) là tâm đường tròn ngoại tiếp tam giác \(ABC\).
Lời giải chi tiết
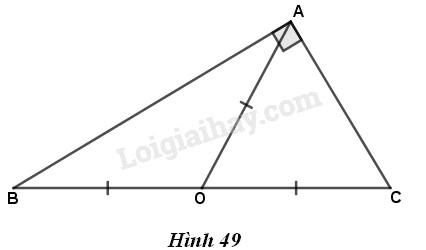
Ta đã biết: Tâm đường tròn ngoại tiếp một tam giác là giao điểm của ba đường trung trực.
Mặt khác theo bài 51, trong một tam giác vuông, hai đường trung trực của hai cạnh góc vuông giao nhau tại trung điểm của cạnh huyền. Do đó, trung điểm của cạnh huyền cũng là điểm chung của ba đường trung trực hay điểm đó chính là tâm đường tròn ngoại tiếp tam giác.
Do tâm đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền nên đường trung tuyến xuất phát từ đỉnh góc vuông của một tam giác vuông bằng bán kính đường tròn ngoại tiếp và bằng \(\dfrac{1}{2}\) cạnh huyền (đường kính đường tròn ngoại tiếp). Trong hình vẽ, \(AO\) là đường trung tuyến xuất phát từ đỉnh góc vuông của tam giác \(ABC\) và \(AO=\dfrac{1}{2}BC\).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 53 trang 96 Vở bài tập toán 7 tập 2
- Bài 51 trang 94 Vở bài tập toán 7 tập 2
- Bài 50 trang 94 Vở bài tập toán 7 tập 2
- Bài 49 trang 93 Vở bài tập toán 7 tập 2
- Bài 48 trang 93 Vở bài tập toán 7 tập 2
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
