Phần hình học - Ôn tập cuối năm

Bài 4 trang 115 Vở bài tập toán 7 tập 2


Giải bài 4 trang 115, 116 VBT toán 7 tập 2. Cho tam giác cân ADC (AD = DC) có góc ACD bằng 31 độ. Trên cạnh AC lấy một điểm B sao cho góc ABD bằng 88 độ. Từ C kẻ một tia song song với ...

Đề bài

Cho tam giác cân \(ADC\) (\(AD = DC\)) có  \(\widehat {ACD} = {31^o}\). Trên cạnh \(AC\) lấy một điểm \(B\) sao cho  \(\widehat {ABD} = {88^o}\). Từ \(C\) kẻ một tia song song với \(BD\) cắt tia \(AD\) ở \(E.\)

a) Hãy tính các góc \(DCE\) và \(DEC;\)

b) Trong tam giác \(CDE\), cạnh nào lớn nhất ? Tại sao?

Phương pháp giải - Xem chi tiết

- Áp dụng định lí tổng ba góc trong tam giác.

-  Áp dụng tính chất hai đường thẳng song song: Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong bằng nhau; hai góc đồng vị bằng nhau; hai góc trong cùng phía bù nhau.

- Áp dụng mối quan hệ giữa góc và cạnh đối diện trong tam giác.

Lời giải chi tiết

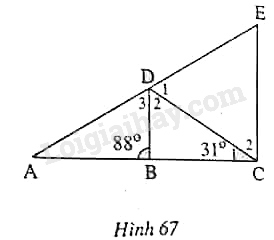
a) \(\widehat {ABD}\) là góc ngoài tại đỉnh \(B\) của tam giác \(DBC\) nên \(\widehat {D_2} =\widehat {ABD}-\widehat {C_1}\)\(=88^o-31^o = {57^o} \).

Vì \(BD//CE\) nên \(\widehat {C_2}=\widehat {D_2}\) \(= {57^o}\) (so le trong)

Vậy \(\widehat {DCE} = {57^o}\)

Tam giác \(ADC\) cân tại \(D\) nên \(\widehat {A}=\widehat {C_1}\) \(= {31^o}\)

Trong tam giác \(ABD\), \(\widehat {D_3} = {180^o} - \widehat {A}-\widehat {ABD}\)\(={180^o}-{31^o}-{88^o}\)\(={61^o}\)

Vì \(BD // CE\) nên \(\widehat {E} = \widehat {D_3} = {61^o}\) (hai góc đồng vị)

Vậy \(\widehat {DEC} = {61^o}\).

b) \(\Delta CDE\) có \(\widehat {DCE} = {57^o}\); \(\widehat {DEC} = {61^o}\) nên \(\widehat {CDE} = {180^o}-{57^o}-{61^o}={62^o}\)

 Theo quan hệ giữa góc và cạnh đối diện của một tam giác ta có cạnh \(CE\) (đối diện với góc \(CDE\)) là cạnh lớn nhất.

Loigiaihay.com


Bình chọn:
4.3 trên 12 phiếu
Bài tiếp theo

>> Xem thêm

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store