-
GIẢI TÍCH SBT - TOÁN 12
-
HÌNH HỌC SBT - TOÁN 12
Bài 2.30 trang 63 SBT hình học 12
Giải bài 2.30 trang 63 sách bài tập hình học 12. Cho đường tròn tâm O bán kính r’. Xét hình chóp S.ABCD có SA vuông góc với mặt phẳng đáy, S và A cố định, SA = h cho trước và có đáy ABCD là một tứ giác tùy ý nội tiếp đường tròn đã cho, trong đó các đường chéo AC và BD vuông góc với nhau.
Đề bài
Cho đường tròn tâm \(O\) bán kính \(r’\). Xét hình chóp \(S.ABCD\) có \(SA\) vuông góc với mặt phẳng đáy, \(S\) và \(A\) cố định, \(SA = h\) cho trước và có đáy \(ABCD \) là một tứ giác tùy ý nội tiếp đường tròn đã cho, trong đó các đường chéo \(AC\) và \(BD\) vuông góc với nhau.
a) Tính bán kính \(r\) của mặt cầu đi qua năm đỉnh của hình chóp.
b) Hỏi đáy \(ABCD\) là hình gì để thể tích hình chóp đạt giá trị lớn nhất?
Phương pháp giải - Xem chi tiết
a) Xác định tâm mặt cầu (cách đều năm điểm \(S,A,B,C,D\)) và tính bán kính.
b) Viết công thức tính thể tích khối chóp. Đánh giá GTLN của thể thích và kết luận.
Lời giải chi tiết
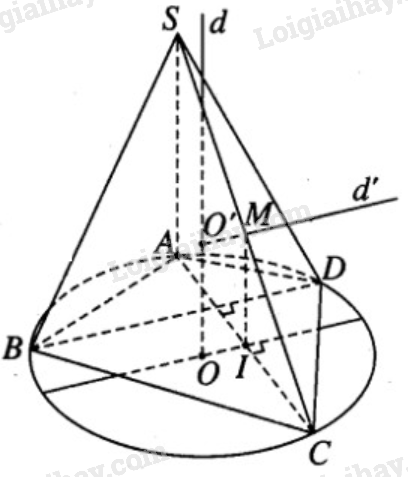
a) Trong mặt phẳng chứa đường tròn tâm O ngoại tiếp tứ giác ABCD ta kẻ đường kính qua O vuông góc với dây cung AC tại I.
Ta có IA = IC và OI // BD. Gọi O’ là tâm mặt cầu đi qua 5 đỉnh của hình chóp.
Khi đó điểm O’ phải nằm trên trục d của đường tròn ngoại tiếp tứ giác ABCD.
Ta có \(\displaystyle d \bot (ABCD)\) tại O. Gọi M là trung điểm của cạnh SC.
Ta có MI // SA nên \(\displaystyle MI \bot (ABCD)\) tại I. Từ M kẻ đường thẳng d’//OI cắt d tại O’.
Vì \(\displaystyle d' \bot (SAC)\) tại M nên ta có O’C = O’S và O’C là bán kính r của mặt cầu ngoại tiếp hình chóp S.ABCD
Ta có \(\displaystyle r = O'C = \sqrt {OO{'^2} + O{C^2}} = \sqrt {M{I^2} + r{'^2}}\)
\(\displaystyle = \sqrt {{{({h \over 2})}^2} + r{'^2}} \) \(\displaystyle = {{\sqrt {{h^2} + 4r{'^2}} } \over 2}\)
b) Vì SA không đổi nên ta có VSABCD lớn nhất khi và chỉ khi SABCD lớn nhất.
Ta có \(\displaystyle {S_{ABCD}} = {1 \over 2}AC.BD\) trong đó AC và BD là hai dây cung vuông góc với nhau.
Vậy AC.BD lớn nhất khi và chỉ khi AC = BD = 2r’ , nghĩa là tứ giác ABCD là một hình vuông.
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 2.31 trang 63 SBT hình học 12
- Bài 2.32 trang 63 SBT hình học 12
- Bài 2.29 trang 63 SBT hình học 12
- Bài 2.28 trang 62 SBT hình học 12
- Bài 2.27 trang 62 SBT hình học 12
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
