-
ĐẠI SỐ - SBT TOÁN 10 NÂNG CAO
-
Chương 1: Mệnh đề - Tập hợp
-
Chương 2: Hàm số
-
CHƯƠNG III. PHƯƠNG TRÌNH BẬC NHẤT VÀ BẬC HAI
- Bài 1. Đại cương về phương trình
- Bài 2. Phương trình bậc nhất và bậc hai một ẩn
- Bài 3. Một số phương trình quy về phương trình bậc nhất hoặc bậc hai
- Bài 4. Phương trình và hệ phương trình bậc nhất nhiều ẩn
- Bài 5. Một số ví dụ về hệ phương trình bậc hai hai ẩn
- Bài tập Ôn tập chương III - Phương trình bậc nhất và bậc hai
-
CHƯƠNG IV. BẤT ĐẲNG THỨC VÀ BẤT PHƯƠNG TRÌNH
- Bài 1. Bất đẳng thức và chứng minh bất đẳng thức
- Bài 2. Đại cương về bất phương trình
- Bài 3. Bất phương trình và hệ bất phương trình bậc nhất một ẩn
- Bài 4. Dấu của nhị thức bậc nhất
- Bài 5. Bất phương trình và hệ bất phương trình bậc nhất hai ẩn
- Bài 6. Dấu của tam thức bậc hai
- Bài 7. Bất phương trình bậc hai
- Bài 8. Một số phương trình và bất phương trình quy về bậc hai
- Bài tập Ôn tập chương IV - Bất đẳng thức và bất phương trình
-
CHƯƠNG V. THỐNG KÊ
-
CHƯƠNG VI. GÓC LƯỢNG GIÁC VÀ CÔNG THỨC LƯỢNG GIÁC
-
BÀI TẬP ÔN TẬP CUỐI NĂM - ĐẠI SỐ 10 NÂNG CAO
-
-
HÌNH HỌC-SBT TOÁN 10 NÂNG CAO
Câu 12 trang 240 SBT Đại số 10 Nâng cao
Giải bài tập Câu 12 trang 240 SBT Đại số 10 Nâng cao
Đề bài
Dùng đồ thị để biện luận số nghiệm của phương trình:
\({x^2} - 6x + 3 + m = 0.\)
Lời giải chi tiết
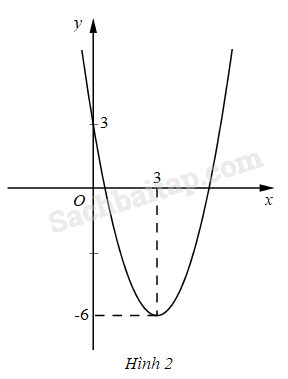
Xét hàm số \(y = f\left( x \right) = {x^2} - 6x + 3.\) Đồ thị hàm số là một parabol quay bề lõm lên trên (h.2) và đỉnh parabol là điểm \(P\left( {3; - 6} \right)\).
Do đó parabol có phương trình \(y = {x^2} - 6x + 3\) và đường thẳng có phương trình \(y = - m:\)
+ Có một điểm chung duy nhất khi \(m = 6;\)
+ Có hai điểm chung phân biệt khi \(m < 6;\)
+ Không có điểm chung khi \(m > 6.\)
Suy ra phương trình \({x^2} - 6x + 3 + m = 0\)
+ Có nghiệm kép khi \(m = 6;\)
+Có hai nghiệm phân biệt khi \(m < 6;\)
+ Vô nghiệm khi \(m > 6.\)
Loigiaihay.com
Bình luận
Chia sẻ
- Câu 13 trang 240 SBT Đại số 10 Nâng cao
- Câu 14 trang 240 SBT Đại số 10 Nâng cao
- Câu 15 trang 240 SBT Đại số 10 Nâng cao
- Câu 16 trang 240 SBT Đại số 10 Nâng cao
- Câu 17 trang 240 SBT Đại số 10 Nâng cao
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
