Giải toán 10, giải bài tập Toán 10 Nâng cao, đầy đủ đại số giải tích và hình học

ÔN TẬP CUỐI NĂM ĐẠI SỐ - TOÁN 10 NÂNG CAO

Bài 8 trang 222 SGK Đại số 10 Nâng cao

Biện luận theo tham số m số nghiệm và dấu các nghiệm của phương trình

Lựa chọn câu để xem lời giải nhanh hơn

LG a
LG b

Biện luận theo tham số m số nghiệm và dấu các nghiệm của phương trình

LG a

x² + 4(m + 3)x + 6(m² – 5m + 6) = 0

Lời giải chi tiết:

Ta có:

Δ’ = 4(m + 3)² – 6(m² – 5m + 6)

= -2m² + 54m=0

$\Leftrightarrow \left[ \begin{array}{l} m = 0\\ m = 27 \end{array} \right.$

S = 4(m + 3)=0 $\Leftrightarrow m = - 3$ ;

P = 6(m² – 5m + 6)=0

$\Leftrightarrow \left[ \begin{array}{l} m = 2\\ m = 3 \end{array} \right.$

Bảng xét dấu:

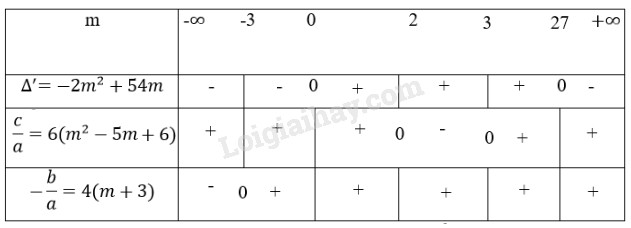
Bảng trên dẫn đến kết luận sau:

+ Nếu m < 0 hoặc m > 27 thì Δ’ < 0 nên phương trịnh vô nghiệm.

+ Nếu m = 0 hoặc m = 27 thì $\Delta ' = 0;\,\,{c \over a} > 0;\,\, - {b \over a} > 0$ nên phương trình có một nghiệm dương (nghiệm kép)

+ Nếu 0 < m < 2 hoặc 3 < m < 27 thì $\Delta ' > 0;\,\,{c \over a} > 0;\,\, - {b \over a} > 0$ nên phương trình có hai nghiệm dương phân biệt.

+ Nếu 2 < m < 3 thì ${c \over a} < 0$ nên phương trình có hai nghiệm trái dấu.

+ Nếu m = 2 hoặc m = 3 thì ${c \over a} = 0\,\,;{{ - b} \over a} > 0$ nên phương trình có một nghiệm bằng 0 và một nghiệm dương.

LG b

(m – 1)x² – (m – 3)x – m – 3 = 0

Lời giải chi tiết:

Khi m = 1, ta có phương trình 2x – 4 = 0. Phương trình có một nghiệm dương.

Khi m ≠ 1, ta có phương trình bậc hai. Số nghiệm và dấu của các nghiệm phụ thuộc vào dấu của các biểu thức sau:

$\eqalign{ & \Delta = {(m - 3)^2} + 4(m - 1)(m + 3) \cr&= 5{m^2} + 2m - 3 \cr & P = {c \over a} = {{ - m - 3} \over {m - 1}} \cr & S = - {b \over a} = {{m - 3} \over {m - 1}} \cr}$

Ta có bảng xét dấu:

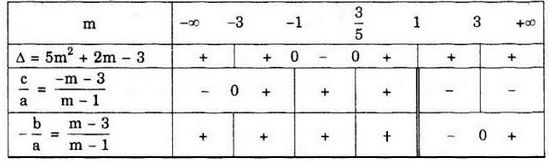
Từ bảng xét dấu, ta suy ra:

+ Nếu $- 1 < m < {3 \over 5}$ thì Δ < 0 nên phương trình vô nghiệm

+ Nếu m < -3 hoặc m > 1 thì ${c \over a} < 0$ nên phương trình có hai nghiệm trái dấu.

+ Nếu -3 < m < -1 hoặc ${3 \over 5} < m < 1$ thì $\Delta > 0;\,{c \over a} > 0;\,{{ - b} \over a} > 0$ nên phương trình có hai nghiệm dương phân biệt.

+ Nếu m = -3 thì $\,{c \over a} = 0;\,{{ - b} \over a} > 0$ nên phương trình có một nghiệm x = 0, nghiệm kia là nghiệm dương

+ Nếu m = -1 hoặc $m = {3 \over 5}$ thì $\Delta = 0;\,{c \over a} > 0;\,{{ - b} \over a} > 0$ nên phương trình có một nghiệm kép dương.

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

3.8 trên 4 phiếu

Bài tiếp theo

Bài 9 trang 222 SGK Đại số 10 Nâng cao
Giải và biện luận các phương trình
Bài 10 trang 222 SGK Đại số 10 Nâng cao
Xét dấu các nghiệm phương trình đó tùy theo m
Bài 11 trang 222 SGK Đại số 10 Nâng cao
Giải và biện luận các hệ phương trình
Bài 12 trang 222 SGK Đại số 10 Nâng cao
Giải các hệ phương trình
Bài 13 trang 222 SGK Đại số 10 Nâng cao
Chứng minh rằng:
Bài 14 trang 222 SGK Đại số 10 Nâng cao
Tìm giá trị nhỏ nhất của các hàm số sau
Bài 15 trang 222 SGK Đại số 10 Nâng cao
Tìm giá trị lớn nhất của hàm số: f(x) = (2 - x)(2x + 1)trên (-0,5; 2)
Bài 16 trang 222 SGK Đại số 10 Nâng cao
Giải các hệ bất phương trình
Bài 17 trang 222 SGK Đại số 10 Nâng cao
Giải các phương trình
Bài 18 trang 223 SGK Đại số 10 Nâng cao
Giải các bất phương trình
Bài 19 trang 223 SGK Đại số 10 Nâng cao
Điểm thi của 32 học sinh trong kỳ thi tiếng anh (thang điểm 100) như sau:
Bài 20 trang 223 SGK Đại số 10 Nâng cao
Một siêu thị thu được các số liệu sau đây về số tiền (đơn vị: nghìn đồng) mà mỗi người đã mua ở đây:
Bài 21 trang 223 SGK Đại số 10 Nâng cao
Tuổi của 60 cán bộ trong một cơ quan được thống kê và trình bày trong bảng phân bố tần số ghép lớp sau:
Bài 22 trang 224 SGK Đại số 10 Nâng cao
Hãy tính các giá trị lượng giác của góc α
Bài 23 trang 224 SGK Đại số 10 Nâng cao
Chứng minh các đẳng thức sau:
Bài 24 trang 224 SGK Đại số 10 Nâng cao
Chứng minh rằng:
Bài 25 trang 224 SGK Đại số 10 Nâng cao
Tìm các số c và β sao cho: sinα + cosα =c.sin(α + β) với mọi α
Bài 7 trang 221 SGK Đại số 10 Nâng cao
Không giải phương trình, tính gần đúng tổng các bình phương hai nghiệm của phương trình (chính xác đến hàng phần trăm)
Bài 6 trang 221 SGK Đại số 10 Nâng cao
Tính k biết rằng (1) có 2 nghiệm trùng nhau
Bài 5 trang 221 SGK Đại số 10 Nâng cao
Khi (d) và (P) cắt nhau, gọi A và B là giao điểm, hãy tìm tọa độ trung điểm của đoạn thẳng AB
Bài 4 trang 221 SGK Đại số 10 Nâng cao
Tại sao (Ho) có tâm đối xứng là gốc tọa độ O?
Bài 3 trang 221 SGK Đại số 10 Nâng cao
Cho hai đường thẳng (d1): y = mx - 3 và (d2): x + y = m
Bài 2 trang 221 SGK Đại số 10 Nâng cao
Tìm tập xác định và xét tính chẵn – lẻ của mỗi hàm số sau:
Bài 1 trang 220 SGK Đại số 10 Nâng cao
Cho các tập con của tập số thực R: A = [-1; 1], B = [a;b) và C = (-∞;c) Trong đó a, b (a < b) và c là các số thực

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Click để xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.