Giải bài tập Toán 12 Nâng cao, Toán 12 Nâng cao, đầy đủ giải tích và hình học Bài 1. Hệ tọa độ trong không gian

Bài 12 trang 82 SGK Hình học 12 Nâng cao


Cho hình chóp S.ABC có đường cao SA = h, đáy là tam giác ABC vuông tại C, AC = b, BC = a. Gọi M là trung điểm của AC và N là điểm sao cho . a) Tính độ dài đoạn thẳng MN. b) Tìm sự liên hệ giữa a, b, h để MN vuông góc với SB.

Lựa chọn câu để xem lời giải nhanh hơn

Cho hình chóp S.ABC có đường cao SA = h, đáy là tam giác ABC vuông tại C, AC = b, BC = a. Gọi M là trung điểm của AC và N  là điểm sao cho \(\overrightarrow {SN}  = {1 \over 3}\overrightarrow {SB} \).

LG a

Tính độ dài đoạn thẳng MN.

Phương pháp giải:

Chọn hệ trục Oxyz sao cho A trùng O, tia AC trùng tia Ox, AS trùng Oz.

Tìm tọa độ các điểm và tính toán.

Lời giải chi tiết:

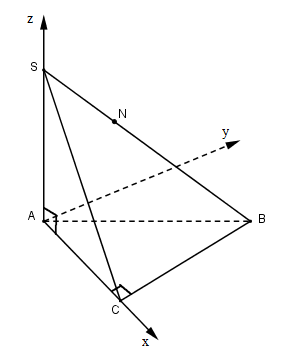
Chọn hệ trục Oxyz như hình vẽ, B nằm trong góc xOy.
Ta có: \(A = \left( {0;0;0} \right),C = \left( {b;0;0} \right),\) \(B = \left( {b;a;0} \right),S = \left( {0;0;h} \right)\) .

\(M\left( {{b \over 2};0;0} \right),\overrightarrow {SB}  = \left( {b;a; - h} \right)\)

Gọi \(N\left( {x;y;z} \right)\) thì \(\overrightarrow {SN}  = \left( {x;y;z - h} \right)\).

\(\overrightarrow {SN} = {1 \over 3}\overrightarrow {SB} \Leftrightarrow \left\{ \matrix{
x = {b \over 3} \hfill \cr 
y = {a \over 3} \hfill \cr 
z - h = {{ - h} \over 3} \hfill \cr} \right. \) \(\Leftrightarrow \left\{ \matrix{
x = {b \over 3} \hfill \cr 
y = {a \over 3} \hfill \cr 
z = {{2h} \over 3} \hfill \cr} \right. \) \(\Rightarrow N\left( {{b \over 3};{a \over 3};{{2h} \over 3}} \right)\)

\(\eqalign{
& \overrightarrow {MN} = \left( {{b \over 3} - {b \over 2};{a \over 3};{{2h} \over 3}} \right) \cr &= \left( { - {b \over 6};{a \over 3};{{2h} \over 3}} \right) \cr 
& MN = \sqrt {{{{b^2}} \over {36}} + {{{a^2}} \over 9} + {{4{h^2}} \over 9}} \cr &= {1 \over 6}\sqrt {{b^2} + 4{a^2} + 16{h^2}} \cr} \)

LG b

Tìm sự liên hệ giữa a, b, h để MN vuông góc với SB.

Phương pháp giải:

\(MN \bot SB \Leftrightarrow \overrightarrow {MN} .\overrightarrow {SB}  = 0\)

Lời giải chi tiết:

\(MN \bot SB \Leftrightarrow \overrightarrow {MN} .\overrightarrow {SB}  = 0\) \(\Leftrightarrow  - {{{b^2}} \over 6} + {{{a^2}} \over 3} + {{ - 2{h^2}} \over 3} = 0 \) \(\Leftrightarrow 4{h^2} = 2{a^2} - {b^2}\)

Loigiaihay.com


Bình chọn:
3.6 trên 5 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay

Báo lỗi - Góp ý

>> Luyện thi TN THPT & ĐH năm 2022 trên trang trực tuyến Tuyensinh247.com. Học mọi lúc, mọi nơi với Thầy Cô giáo giỏi, đầy đủ các khoá: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng; Tổng ôn chọn lọc.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua