Bài 11 trang 191 SGK Đại số và Giải tích 12 Nâng cao
Hỏi mỗi số sau đây là số thực hay số ảo (z là số phức tùy ý cho trước sao cho biểu thức xác định)?
Đề bài
Hỏi mỗi số sau đây là số thực hay số ảo (z là số phức tùy ý cho trước sao cho biểu thức xác định)?
\({z^2} + {\left( {\overline z } \right)^2}\); \({{z - \overline z } \over {{z^3} + {{\left( {\overline z } \right)}^3}}}\); \({{{z^2} - {{\left( {\overline z } \right)}^2}} \over {1 + z\overline z }}\)
Phương pháp giải - Xem chi tiết
Sử dụng tính chất:
+) Số phức z là số thực khi và chỉ khi \(\overline z=z \)
+) "Số phức z là số ảo khi và chỉ khi \( \overline z=-z\)
Lời giải chi tiết
* Ta có:
\(\overline {{z^2} + {{\left( {\overline z } \right)}^2}} \\= \overline {{z^2}} + \overline {{{\left( {\overline z } \right)}^2}} \\= {\left( {\overline z } \right)^2} + {\left( {\overline {\overline z } } \right)^2} \\= {\left( {\overline z } \right)^2} + {z^2}\)
\( \Rightarrow {z^2} + {\left( {\overline z } \right)^2}\) là số thực.
Cách khác: Gọi \(z=a+bi\)
Ta có: \({z^2} + {\overline z ^2} = {\left( {a + bi} \right)^2} + {\left( {a - bi} \right)^2} \) \( = {a^2} + 2abi - {b^2} + {a^2} - 2abi - {b^2} \) \(= 2{a^2} - 2{b^2}\)
\(= 2\left( {{a^2} - {b^2}} \right)\) là số thực
* \(\overline {\left( {{{z - \overline z } \over {{z^3} + {{\left( {\overline z } \right)}^3}}}} \right)} \) \( = \frac{{\overline {z - \overline z } }}{{\overline {{z^3} + {{\left( {\overline z } \right)}^3}} }} \) \( = \frac{{\overline z - \overline {\overline z } }}{{\overline {{z^3}} + \overline {{{\left( {\overline z } \right)}^3}} }} \) \(= \frac{{\overline z - z}}{{{{\left( {\overline z } \right)}^3} + {{\left( {\overline {\overline z } } \right)}^3}}} \) \(= - \frac{{z - \overline z }}{{{{\left( {\overline z } \right)}^3} + {z^3}}}\)
\(\Rightarrow {{z - \overline z } \over {{z^3} + {({\overline z })^3}}}\) là số ảo.
* \(\overline {\left( {{{{z^2} - {{\left( {\overline z } \right)}^2}} \over {1 + z\overline z }}} \right)} \) \(= {{{({\overline z })^2} - {z^2}} \over {1 + \overline z z}} \) \(= - {{{z^2}-{({\overline z })^2}} \over {1 + \overline z .z}} \)
\(\Rightarrow {{{z^2} - {{\left( {\overline z } \right)}^2}} \over {1 + z\overline z }}\) là số ảo.
Cách khác:
Loigiaihay.com





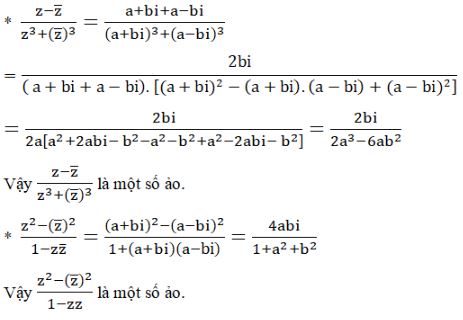








Danh sách bình luận