Bài 1.31 trang 20 SBT hình học 12

Giải bài 1.31 trang 20 sách bài tập hình học 12. Tính thể tích khối lăng trụ có chiều cao bằng h, đáy là ngũ giác đều nội tiếp trong một đường tròn bán kính r.

Đề bài

Tính thể tích khối lăng trụ có chiều cao bằng \(h\), đáy là ngũ giác đều nội tiếp trong một đường tròn bán kính \(r\).

Phương pháp giải - Xem chi tiết

- Tính diện tích đáy ngũ giác đều bằng cách chia đáy thành \(5\) tam giác cân.

- Tính thể tích theo công thức \(V = Bh\).

Lời giải chi tiết

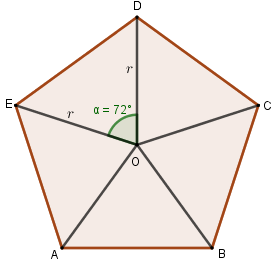
Chia đáy của hình lăng trụ đã cho thành năm tam giác cân có chung đỉnh \(O\) là tâm đường tròn ngoại tiếp đáy.

Ta có: \({S_{ODE}} = \dfrac{1}{2}OD.OE.\sin \widehat {DOE}\) \( = \dfrac{1}{2}{r^2}\sin {72^0}\).

\( \Rightarrow {S_{ABCDE}} = \dfrac{5}{2}{r^2}\sin {72^0}\). Do đó thể tích lăng trụ: \(V = \dfrac{5}{2}h{r^2}\sin {72^0}\).

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Bài 1.32 trang 20 SBT hình học 12
Giải bài 1.32 trang 20 sách bài tập hình học 12. Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD, các mặt (SAB) và (SAD) vuông góc với đáy. Góc giữa mặt (SAC) và đáy bằng 60, AB = 2a , BC = a. Tính thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng AB và SC theo a.
Bài 1.33 trang 20 SBT hình học 12
Giải bài 1.33 trang 20 sách bài tập hình học 12. Cho tứ diện đều ABCD. Gọi (H) là hình bát diện đều có các đỉnh là trung điểm các cạnh của tứ diện đều đó. Tính tỉ số...
Bài 1.34 trang 20 SBT hình học 12
Giải bài 1.34 trang 20 sách bài tập hình học 12. Cho tứ diện ABCD. Gọi hA, hB, hC, hD...
Bài 1.30 trang 20 SBT hình học 12
Giải bài 1.30 trang 20 sách bài tập hình học 12. Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác vuông cân ở C. Cạnh B’B = a và tạo với đáy một góc bằng 600. Hình chiếu vuông góc hạ từ B’ lên đáy trùng với trọng tâm của tam giác ABC. Tính thể tích khối lăng trụ đó theo a.
Bài 1.29 trang 20 SBT hình học 12
Giải bài 1.29 trang 20 sách bài tập hình học 12. Chứng minh rằng mỗi đỉnh của một hình đa diện là đỉnh chung của ít nhất ba cạnh.
Bài 1.28 trang 20 SBT hình học 12
Giải bài 1.28 trang 20 sách bài tập hình học 12. Hình được tạo thành từ hình lập phương ABCD.A’B’C’D’ khi ta bỏ đi các điểm trong của mặt phẳng (ABCD) có phải là một hình đa diện không?