-
GIẢI TÍCH SBT - TOÁN 12
-
HÌNH HỌC SBT - TOÁN 12
Bài 1.2 trang 9 SBT hình học 12
Giải bài 1.2 trang 9 sách bài tập hình học 12. Cho lăng trụ ABC.A’B’C’ . Gọi E, F, G lần lượt là trung điểm của AA’ , BB’, CC’. Chứng minh rằng các lăng trụ ABC.EFG và EFG.A’B’C’ bằng nhau
Đề bài
Cho lăng trụ \(ABC.A’B’C’\) . Gọi \(E, F, G\) lần lượt là trung điểm của \(AA’ , BB’, CC’\). Chứng minh rằng các lăng trụ \(ABC.EFG\) và \(EFG.A’B’C’\) bằng nhau.
Phương pháp giải - Xem chi tiết
Dùng phép tịnh tiến vecto \(\overrightarrow{AE}\) biến lăng trụ \(ABC.EFG\) thành lăng trụ \(EFG.A’B’C\).
Quảng cáo
Lời giải chi tiết
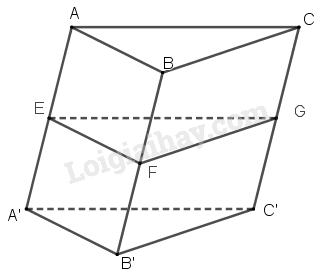
Vì \( E, F, G\) lần lượt là trung điểm của \(AA’, BB’, CC’\) nên ta có:
Ta có: \(T_{\overrightarrow{AE}}(A)=E\); \(T_{\overrightarrow{AE}}(B)=F\); \(T_{\overrightarrow{AE}}(C)=G\)
\(T_{\overrightarrow{AE}}(E)=A’\); \(T_{\overrightarrow{AE}}(F)=B’\); \(T_{\overrightarrow{AE}}(G)=C’\)
\(\Rightarrow T_{\overrightarrow{AE}}(ABC.EFG)=EFG.A’B’C’\).
Vậy lăng trụ \(ABC.EFG\) và \(EFG.A’B’C’\) bằng nhau.
Loigiaihay.com
Bình luận
Chia sẻ
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
