Giải bài tập Toán 12 Nâng cao, Toán 12 Nâng cao, đầy đủ giải tích và hình học Ôn tập chương III - Nguyên hàm, tích phân và ứng dụng

Bài 52 Trang 177 SGK Đại số và Giải tích 12 Nâng cao


Tính diện tích của các hình phẳng giới hạn bởi:

Lựa chọn câu để xem lời giải nhanh hơn

Tính diện tích của các hình phẳng giới hạn bởi:

LG a

Parabol \(y = {x^2} - 2x + 2,\) tiếp tuyến của nó tại điểm \(M(3;5)\) và trục tung

Phương pháp giải:

- Viết phương trình tiếp tuyến.

- Dựng hình suy ra công thức tính diện tích.

Lời giải chi tiết:

 

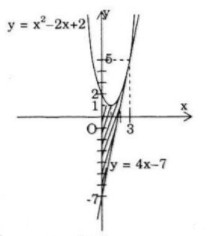
Ta có \(y' = 2x - 2 \Rightarrow y'\left( 3 \right) = 4.\)
Phương trình tiếp tuyến với parabol tại M(3;5) là:
\(y - 5 = 4\left( {x - 3} \right) \Leftrightarrow y = 4x - 7\)
Gọi S là diện tích cần tìm, ta có :

\(\eqalign{
& S = \int\limits_0^3 {\left( {{x^2} - 2x + 2 - 4x + 7} \right)} dx \cr 
& \,\,\, = \int\limits_0^3 {\left( {{x^2} - 6x + 9} \right)} dx = \int\limits_0^3 {{{\left( {x - 3} \right)}^2}dx} \cr 
& \,\,\, = \left. {{1 \over 3}{{\left( {x - 3} \right)}^3}} \right|_0^3 = 9. \cr} \)

LG b

Parabol \(y =  - {x^2} + 4x - 3\) và các tiếp tuyến của nó tại các điểm \(A(0;-3)\) và \(B(3;0)\)

Phương pháp giải:

- Viết phương trình tiếp tuyến.

- Dựng hình suy ra công thức tính diện tích.

Lời giải chi tiết:

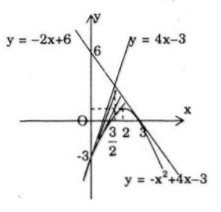
Ta có \(y' =  - 2x + 4 \) \(\Rightarrow y'\left( 0 \right) = 4;y'\left( 3 \right) =  - 2\)
Phương trình tiếp tuyến tại \(A(0;-3)\) là :
\(y + 3 = 4\left( {x - 0} \right) \Leftrightarrow y = 4x - 3\)
Phương trình tiếp tuyến tại \(B(3;0)\) là :
\(y =  - 2\left( {x - 3} \right) \Leftrightarrow y =  - 2x + 6\)
Giao điểm của hai tiếp tuyến là \(C\left( {{3 \over 2};3} \right).\) 

Kí hiệu \({A_1}\) và \({A_2}\) là tam giác cong \(ACD\) Và \(BCD\). Ta có :

\(S\left( {{A_1}} \right) = \int\limits_0^{{3 \over 2}} {\left( {4x - 3 + {x^2} - 4x + 3} \right)} dx \) \(= \int\limits_0^{{3 \over 2}} {{x^2}dx = \left. {{{{x^3}} \over 3}} \right|_0^{{3 \over 2}}}  = {9 \over 8}\)

\(S\left( {{A_2}} \right) = \int\limits_{{3 \over 2}}^3 {\left( { - 2x + 6 + {x^2} - 4x + 3} \right)} dx \) \(= \int\limits_{{3 \over 2}}^3 {{{\left( {x - 3} \right)}^2}dx = } \left. {{1 \over 3}{{\left( {x - 3} \right)}^3}} \right|_{{3 \over 2}}^3 = {9 \over 8}\)

Vậy \(S = S\left( {{A_1}} \right) + S\left( {{A_2}} \right) = {9 \over 8} + {9 \over 8} = {9 \over 4}\)

 Loigiaihay.com


Bình chọn:
3.7 trên 6 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay

Báo lỗi - Góp ý

Group Ôn Thi ĐGNL & ĐGTD Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store