 Giải bài tập Toán 12 Nâng cao, Toán 12 Nâng cao, đầy đủ giải tích và hình học
Giải bài tập Toán 12 Nâng cao, Toán 12 Nâng cao, đầy đủ giải tích và hình học
 Ôn tập chương III - Nguyên hàm, tích phân và ứng dụng
Ôn tập chương III - Nguyên hàm, tích phân và ứng dụng
Bài 50 Trang 176 SGK Đại số và Giải tích 12 Nâng cao
Tính các tích phân sau:
Tính các tích phân sau:
LG a
\(\int\limits_0^{{\pi \over 2}} {{x^2}\sin 2xdx;} \)
Phương pháp giải:
Sử dụng phương pháp tích phân từng phần
Đặt\(\left\{ \matrix{u = {x^2} \hfill \cr dv = \sin 2xdx \hfill \cr} \right. \)
Lời giải chi tiết:
Đặt
\(\left\{ \matrix{
u = {x^2} \hfill \cr
dv = \sin 2xdx \hfill \cr} \right. \Rightarrow \left\{ \matrix{
du = 2xdx \hfill \cr
v = - {1 \over 2}\cos 2x \hfill \cr} \right.\)
Do đó \(\int\limits_0^{{\pi \over 2}} {{x^2}\sin 2xdx}\) \( = \left. { - {1 \over 2}{x^2}\cos 2x} \right|_0^{{\pi \over 2}} + \int\limits_0^{{\pi \over 2}} {{x}\cos 2xdx} \)
\( = {{{\pi ^2}} \over 8} + \int\limits_0^{{\pi \over 2}} {x\cos 2xdx\,\,\,\,\,\,\,\left( 1 \right)} \)
Đặt
\(\left\{ \matrix{
u = x \hfill \cr
dv = \cos 2xdx \hfill \cr} \right. \Rightarrow \left\{ \matrix{
du = dx \hfill \cr
v = {1 \over 2}\sin 2x \hfill \cr} \right.\)
Do đó \(\int\limits_0^{{\pi \over 2}} {x\cos 2xdx}\) \( = \left. {\frac{1}{2}x\sin 2x} \right|_0^{\frac{\pi }{2}} - \frac{1}{2}\int\limits_0^{\frac{\pi }{2}} {\sin 2xdx} \) \(= 0 - \left. {\frac{1}{2}.\frac{{ - \cos 2x}}{2}} \right|_0^{\frac{\pi }{2}}\) \(= \left. {{1 \over 4}\cos 2x} \right|_0^{{\pi \over 2}} = - {1 \over 2}\,\,\,\,\,\,\,\,\left( 2 \right)\)
Thay (2) vào (1) ta được: \(\int\limits_0^{{\pi \over 2}} {{x^2}\sin 2xdx = {{{\pi ^2}} \over 8}} - {1 \over 2}.\)
LG b
\(\int\limits_1^2 {x\left( {2{x^2} + 1} \right)} dx;\)
Phương pháp giải:
Đổi biến \(u = 2{x^2} + 1\)
Lời giải chi tiết:
Đặt \(u = 2{x^2} + 1 \Rightarrow du = 4xdx \) \(\Rightarrow xdx = {{du} \over 4}\)
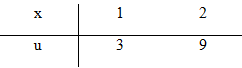
\(\int\limits_1^2 {x\left( {2{x^2} + 1} \right)dx = {1 \over 4}} \int\limits_3^9 {udu} \) \( = \left. {{1 \over 8}{u^2}} \right|_3^9 = 9\)
Cách khác:
\(\int\limits_1^2 {x\left( {2{x^2} + 1} \right)dx} \) \( = \int\limits_1^2 {\left( {2{x^3} + x} \right)dx} \) \( = \left. {\left( {\dfrac{{2{x^4}}}{4} + \dfrac{{{x^2}}}{2}} \right)} \right|_1^2\) \( = 10 - 1 = 9\)
LG c
\(\int\limits_2^3 {\left( {x - 1} \right)} {e^{{x^2} - 2x}}dx.\)
Phương pháp giải:
Đổi biến \(u = {x^2} - 2x\).
Lời giải chi tiết:
Đặt \(u = {x^2} - 2x \Rightarrow du = 2\left( {x - 1} \right)dx \) \(\Rightarrow \left( {x - 1} \right)dx = {{du} \over 2}\)
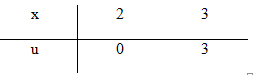
\(\int\limits_2^3 {\left( {x - 1} \right)} {e^{{x^2} - 2x}}dx \) \(= {1 \over 2}\int\limits_0^3 {{e^u}du = } \left. {{1 \over 2}{e^u}} \right|_0^3 = {1 \over 2}\left( {{e^3} - 1} \right).\)
Loigiaihay.com












Danh sách bình luận