 Giải bài tập Toán 12 Nâng cao, Toán 12 Nâng cao, đầy đủ giải tích và hình học
Giải bài tập Toán 12 Nâng cao, Toán 12 Nâng cao, đầy đủ giải tích và hình học
 Ôn tập chương III - Nguyên hàm, tích phân và ứng dụng
Ôn tập chương III - Nguyên hàm, tích phân và ứng dụng
Bài 49 Trang 176 SGK Đại số và Giải tích 12 Nâng cao
Một chất điểm A xuất phát từ vị trí O, chuyển động thẳng nhanh dần đều; 8 giây sau nó đạt đến vận tốc 6 m/s. từ thời điểm đó nó chuyển động thẳng đều. Một chất điểm B xuất phát từ cùng vị trí O nhưng chậm hơn 12 giây so với A và chuyển động thẳng nhanh dần đều. biết rằng B đuổi kịp A sau 8 giây ( kể từ lúc B xuất phát). Tìm vận tốc của B tại thời điểm đuổi kịp A.
Đề bài
Một chất điểm A xuất phát từ vị trí O, chuyển động thẳng nhanh dần đều; 8 giây sau nó đạt đến vận tốc 6 m/s. Từ thời điểm đó nó chuyển động thẳng đều. Một chất điểm B xuất phát từ cùng vị trí O nhưng chậm hơn 12 giây so với A và chuyển động thẳng nhanh dần đều. Biết rằng B đuổi kịp A sau 8 giây (kể từ lúc B xuất phát). Tìm vận tốc của B tại thời điểm đuổi kịp A.
Lời giải chi tiết
Từ công thức v1=v0+at ta có:
Gia tốc trong 8 giây đầu của chất điểm A là:
\(a = \dfrac{{{v_1} - {v_0}}}{t}\) \( = \dfrac{{6 - 0}}{8} = \dfrac{3}{4}\left( {m/{s^2}} \right)\)
⇒ Phương trình vận tốc của chuyển động có dạng:
\(V\left( t \right) = \int {\dfrac{3}{4}dt} = \dfrac{3}{4}t + C\left( {m/{s^2}} \right)\)
Tại t = 0 thì v(0)= 0 nên C= 0.
Do đó,phương trình chuyển động của vật là: \(v\left( t \right) = \dfrac{3}{4}t\)
Trong 8 giây đầu này, chất điểm A chuyển động nhanh dần với vận tốc \(v\left( t \right) = \dfrac{3}{4}t\).
Vậy nó đi được quãng đường là \(\int\limits_0^8 {\dfrac{3}{4}tdt} = \left. {\dfrac{3}{4}.\dfrac{{{t^2}}}{2}} \right|_0^8 = 24\)
Sau 12 giây tiếp theo (khi mà bị B đuổi kịp A), A đi được thêm 6.12 = 72 mét.
Như vậy, khi bị B đuổi kịp, A và B đi được quãng đường là 24 + 72 = 96 mét
Từ công thức \(S = {S_0} + \dfrac{1}{2}a{t^2}\)
Suy ra gia tốc của chất điểm B là: \(a = \dfrac{{2\left( {S - {S_0}} \right)}}{{{t^2}}}\) \( = \dfrac{{2\left( {96 - 0} \right)}}{{{8^2}}} = 3\)
Vậy khi đuổi kịp A, vận tốc của B là:
v1=v0+at=0+3.8=24 (m/s)
Cách khác:
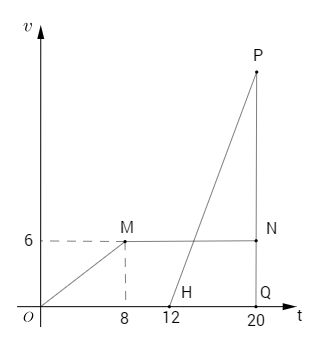
Thời điểm A và B gặp nhau là 20 giây kể từ lúc A xuất phát.
Đồ thị của vận tốc của A là đường gấp khúc OMN.
Quãng đường mà A đi được (s = vt ) là diện tích hình thang OMNQ.
\({S_{OMNQ}} = {1 \over 2}\left( {20 + 12} \right).6 = 96\)
Vậy lúc gặp B, A đi được \(96 m\).
Đồ thị vận tốc của B là đường thẳng HP.
Vì B xuất phát cùng vị trí với A nên B cũng đi được \(96 m\) . Quãng đường B đi được bằng diện tích tam giác \(HPQ\).
Ta có \({S_{HPQ}} = {1 \over 2}.PQ.HQ \) \(\Rightarrow 96 = {1 \over 2}.PQ.8 \Rightarrow PQ = 24.\)
Vậy vận tốc của B tại thời điểm gặp A là \(24\, m/s\).
Loigiaihay.com












Danh sách bình luận