Phần câu hỏi bài 7 trang 47, 48 Vở bài tập toán 7 tập 2

Câu 19

Khoanh tròn vào số là bậc của đa thức.  

Phương pháp giải:

- Thu gọn đa thức nếu có. 

- Bậc của đa thức một biến (khác đa thức không, đã thu gọn) là số mũ lớn nhất của biến trong đa thức đó.

Lời giải chi tiết:

Đa thức \({x^2} + 2x - 3{x^3} + 2{x^5} + 3{x^4} - 1\) có bậc \(5\).

\({x^6} + 2{x^5} - 3{x^6} + 2{x^5} + 2{x^6} - {x^3} + {x^2} \)\(\,+ 1\)

\(= \left( {{x^6} - 3{x^6} + 2{x^6}} \right) + \left( {2{x^5} + 2{x^5}} \right)\)\(\, - {x^3} + {x^2} + 1\)

\(= 4{x^5} - {x^3} + {x^2} + 1\)

Do đó đa thức \({x^6} + 2{x^5} - 3{x^6} + 2{x^5} + 2{x^6} - {x^3} + {x^2} \)\(\,+ 1\) có bậc \(5\).

\({\left( {x - 2} \right)^2} + 2x - 3{x^2} + 3\)

\(= \left( {x - 2} \right)\left( {x - 2} \right) + 2x - 3{x^2} + 3\)

\(= x.x + x.\left( { - 2} \right) + \left( { - 2} \right).x \)\(\,+ \left( { - 2} \right).\left( { - 2} \right)\)\(\, + 2x - 3{x^2} + 3\)

\(= {x^2} - 2x - 2x + 4 + 2x - 3{x^2} + 3\)

\(= \left( {{x^2} - 3{x^2}} \right) + \left( { - 2x - 2x + 2x} \right) \)\(\,+ \left( {4 + 3} \right)\)

\(= - 2{x^2} - 2x + 7\)

Do đó đa thức \({\left( {x - 2} \right)^2} + 2x - 3{x^2} + 3\) có bậc \(2\).

\(\begin{array}{l}
2{x^5} + 3{x^4} - {x^8} + {x^5} + 1\\
= - {x^8} + \left( {2{x^5} + {x^5}} \right) + 3{x^4} + 1\\
= - {x^8} + 3{x^5} + 3{x^4} + 1
\end{array}\)

Do đó đa thức \(2{x^5} + 3{x^4} - {x^8} + {x^5} + 1\) có bậc \(8\).

Ta khoanh như sau:  

Câu 20

Điền vào ô trống trong bảng sau :

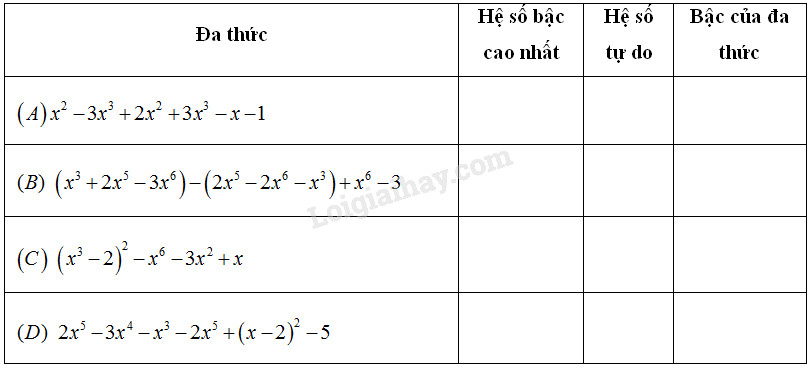
Phương pháp giải:

Ta thu gọn đa thức đã cho sau đó trong dạng thu gọn của đa thức:

- Hệ số của hạng tử có bậc cao nhất gọi là hệ số cao nhất.

- Hệ số của hạng tử bậc không gọi là hệ số tự do. 

Lời giải chi tiết:

\({x^2} - 3{x^3} + 2{x^2} + 3{x^3} - x - 1\)

\(= \left( { - 3{x^3} + 3{x^3}} \right) + \left( {{x^2} + 2{x^2}} \right) - x \)\(\,- 1\)

\(= 3{x^2} - x - 1\)

Hệ số bậc cao nhất là:\(3\)

Hệ số tự do là: \(-1\)

Bậc của đa thức là: \(2\)

\(\left( {{x^3} + 2{x^5} - 3{x^6}} \right) - \left( {2{x^5} - 2{x^6} - {x^3}} \right) \)\(\,+ {x^6} - 3\)

\(= {x^3} + 2{x^5} - 3{x^6} - 2{x^5} + 2{x^6} + {x^3}\)\(\, + {x^6} - 3\)

\(= \left( { - 3{x^6} + 2{x^6} + {x^6}} \right) + \left( {2{x^5} - 2{x^5}} \right) \)\(\,+ \left( {{x^3} + {x^3}} \right) - 3\)

\(= 2{x^3} - 3\)

Hệ số bậc cao nhất là: \(2\)

Hệ số tự do là: \(-3\)

Bậc của đa thức là: \(3\)

\({\left( {{x^3} - 2} \right)^2} - {x^6} - 3{x^2} + x\)

\(= \left( {{x^3} - 2} \right).\left( {{x^3} - 2} \right) - {x^6} - 3{x^2} + x\)

\(= {x^3}.{x^3} + {x^3}.\left( { - 2} \right) + \left( { - 2} \right).{x^3} \)\(\,+ \left( { - 2} \right).\left( { - 2} \right) - {x^6} - 3{x^2} + x\)

\(= {x^6} - 2{x^3} - 2{x^3} + 4 - {x^6} - 3{x^2} + x\)

\(= \left( {{x^6} - {x^6}} \right) + \left( { - 2{x^3} - 2{x^3}} \right) - 3{x^2} \)\(\,+ x + 4\)

\(= - 4{x^3} - 3{x^2} + x + 4\)

Hệ số bậc cao nhất là: \(-4\)

Hệ số tự do là: \(4\)

Bậc của đa thức là: \(3\)

\(2{x^5} - 3{x^4} - {x^3} - 2{x^5} + {\left( {x - 2} \right)^2} - 5\)

\(= 2{x^5} - 3{x^4} - {x^3} - 2{x^5} \)\(\,+ \left( {x - 2} \right).\left( {x - 2} \right) - 5\)

\(= 2{x^5} - 3{x^4} - {x^3} - 2{x^5} + x.x \)\(\,+ x.\left( { - 2} \right) + \left( { - 2} \right).x + \left( { - 2} \right).\left( { - 2} \right)\)\(\, - 5\)

\(= 2{x^5} - 3{x^4} - {x^3} - 2{x^5} + {x^2} \)\(\,- 2x - 2x + 4 - 5\)

\(= \left( {2{x^5} - 2{x^5}} \right) - 3{x^4} - {x^3} + {x^2} \)\(\,+ \left( { - 2x - 2x} \right) - 1\)

\(= - 3{x^4} - {x^3} + {x^2} - 4x - 1\)

Hệ số bậc cao nhất là: \(-3\)

Hệ số tự do là: \(-1\)

Bậc của đa thức là: \(4\)

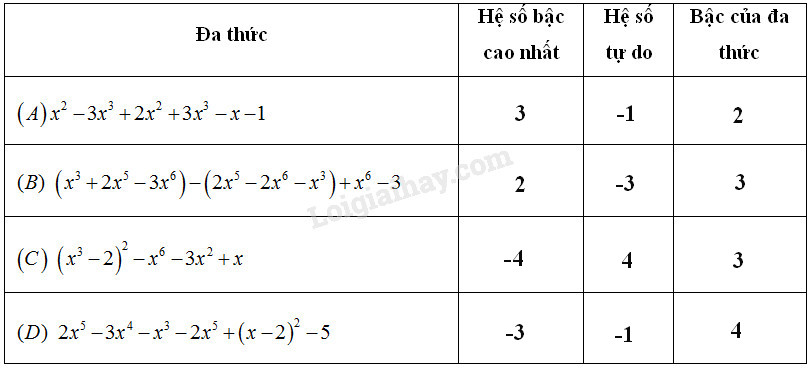
Ta điền vào bảng như sau: 

Câu 21

Điền “\( \times \)” vào ô trống trong bảng sau : 

Phương pháp giải:

- Thay giá trị của biến vào đa thức.

- Tính rồi tích vào ô trống thích hợp. 

Lời giải chi tiết:

(A) Thay \(x =  - 1\) vào đa thức \({x^5} + \dfrac{1}{3}{x^2} - \dfrac{5}{6}{x^4} + 2{x^3} - 6x - 12\) ta được:

\(  {\left( { - 1} \right)^5} + \dfrac{1}{3} \cdot {\left( { - 1} \right)^2} - \dfrac{5}{6} \cdot {\left( { - 1} \right)^4}\)\( + 2.{\left( { - 1} \right)^3} - 6.\left( { - 1} \right) - 12\)

\( =  - 1 + \dfrac{1}{3} - \dfrac{5}{6} - 2 + 6 - 12\)

\( = \) \( - \dfrac{{19}}{2}\)

(B) Với \(x =  - 2\) thì \(5{x^6} - {x^5} - 3x + 4{x^4} - 4{x^3} - 2\)

\( = 5.{\left( { - 2} \right)^6} - {\left( { - 2} \right)^5} - 3.\left( { - 2} \right) \)\(\,+ 4.{\left( { - 2} \right)^4}\)\(- 4.{\left( { - 2} \right)^3} - 2\)

\( = 452\)

(C) Với \(x =  - 1\)thì \(\left| {{x^4} - 5{x^3}} \right| + \left| {{x^5} - 5{x^3}} \right| - \left( {3{x^2} - {x^4}} \right)\)\( + 2008\)

\( = \left| {{{\left( { - 1} \right)}^4} - 5.{{\left( { - 1} \right)}^3}} \right|\)\(\,+ \left| {{{\left( { - 1} \right)}^5} - 5.{{\left( { - 1} \right)}^3}} \right|\)\( - \left[ {3.{{\left( { - 1} \right)}^2} - {{\left( { - 1} \right)}^4}} \right] + 2008\)

\( = \left| 6 \right| + \left| 4 \right| - 2 + 2008\) 

\( = 2016\)

Vậy (A) – Sai;

       (B) – Sai;

       (C) – Đúng. 

Loigiaihay.com