Bài tập cuối chương IV - Từ trường

Bài IV.11* trang 56 SBT Vật Lí 11

Giải bài IV.11* trang 56 SBT Vật Lí 11. Hai dòng điện cường độ I1 = 6,0 A và I2 = 9,0 A có chiều ngược nhau chạy qua hai dây dẫn thẳng dài, song song cách nhau 100 mm trong không khí.

Đề bài

Hai dòng điện cường độ I₁ = 6,0 A và I₂ = 9,0 A có chiều ngược nhau chạy qua hai dây dẫn thẳng dài, song song cách nhau 100 mm trong không khí.

1. Xác định cảm ứng từ do hai dòng điện này gây ra tại :

a) Điểm M, cách I₁ một khoảng 60 mm và cách I₂ một khoảng 40 mm.

b) Điểm N, cách I₁ một khoảng 60 mm và cách I₂ một khoảng 80 mm.

2. Xác định quỹ tích những điểm tại đó cảm ứng từ bằng không

Phương pháp giải - Xem chi tiết

Sử dụng biểu thức tính cảm ứng từ: \( B= 2.10^{-7}\dfrac{I}{r}\)

Lời giải chi tiết

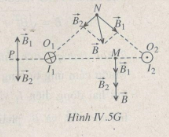
Giả sử hai dòng điện I₁ , I₂ chạy qua hai dây dẫn theo hướng vuông góc với mặt phẳng Hình IV.5G tại hai điểm O_1, O₂

1.a) Xác định cảm ứng từ tại điểm M.

Vì \(MO_1 + MO_2 = 60 + 40 = 100 mm = O_1O_2\) nên điểm M phải nằm trên đoạn thẳng O₁O₂

và ở phía trong O₁O₂

- Cảm ứng từ \(\overrightarrow {{B_1}} \) do dòng điện I₁ gây ra tại M có phương vuông góc với O₁M và có độ lớn :

\({B_1} = {2.10^{ - 7}}.{\dfrac{6,0}{60.10^{ - 3}}} = {2,0.10^{ - 5}}T\)

- Cảm ứng từ \(\overrightarrow {{B_2}} \) do dòng điện I₂ gây ra tại M có phương vuông góc với O₂M và có độ lớn :

\({B_2} = {2.10^{ - 7}}.{\dfrac{9,0}{40.10^{ - 3}}} = {4,5.10^{ - 5}}T\)

Hai vectơ \(\overrightarrow {{B_1}} \) và \(\overrightarrow {{B_2}} \) đều hướng thẳng đứng xuống dưới, nên vectơ cảm ứng từ \(\overrightarrow {{B}} \) tại M cũng hướng thẳng đứng như Hình IV.5G và có độ lớn bằng :

\(B = B_1 + B_2 = 2,0.10^{-5} + 4,5.10^{-5} = 6,5.10^{-5} T\)

b) Xác định cám ứng từ tại điểm N :

Vì cạnh NO₁ = 60 mm, NO₂ = 80 mm, O₁O₂ = 100 mm, có độ dài chia theo tỉ lệ 3 : 4 : 5, nên NO₁O₂ là tam giác vuông tại N, có cạnh huyền O₁O₂

- Cảm ứng từ \(\overrightarrow {{B_1}} \) do dòng điện I₁ gây ra tại N có phương vuông góc với O₁N và có độ lớn :

\({B_1} = {2.10^{ - 7}}.{\dfrac{6,0}{60.10^{ - 3}}} = {2,0.10^{ - 5}}T\)

- Cảm ứng từ \(\overrightarrow {{B_2}} \) do dòng điện I₂ gây ra tại N có phương vuông góc với O₂N và có độ lớn :

\({B_2} = {2.10^{ - 7}}.{\dfrac{9,0}{80.10^{ - 3}}} = {2,25.10^{ - 5}}T\)

Hai vectơ và có phương vuông góc với nhau, nên vectơ cảm ứng từ tại N nằm trùng với đường chéo của hình chữ nhật có hai cạnh và như Hình IV.5G và có độ lớn bằng :

\(B = \sqrt {B_1^2 + B_2^2} = \sqrt {{{({{2,0.10}^{ - 5}})}^2} + {{({{2,25.10}^{ - 5}})}^2}} \approx {3,0.10^{ - 5}}T\)

2. Xác định quỹ tích những điểm p tại đó cảm ứng từ

Muốn cảm ứng từ tổng hợp tại một điểm p nào đó trong từ trường gây ra bởi hai dòng điện I₁ và I₂có giá trị \(\overrightarrow B = \overrightarrow {{B_1}} + \overrightarrow {{B_2}} = \overrightarrow 0 \) hay \(\overrightarrow {{B_1}} = - \overrightarrow {{B_2}} \), thì hai vectơ \(\overrightarrow {{B_1}} \) và \(\overrightarrow {{B_2}} \) phải .cùng phương, ngược chiều và cùng độ lớn.

Các điều kiện này chỉ được thực hiện khi điểm p nằm trên đường thẳng O₁O₂ ( \(\overrightarrow {{B_1}} \) và \(\overrightarrow {{B_2}} \) cùng phương) và nằm bên ngoài khoảng O₁O₂ ( \(\overrightarrow {{B_1}} \) và \(\overrightarrow {{B_2}} \) ngược chiều) tại vị trí ứng với các khoảng cách PO₁ và PO₂ sao cho \(\overrightarrow {{B_1}} \) và \(\overrightarrow {{B_2}} \) có cùng độ lớn.

Vì \({B_1} = {2.10^{ - 7}}.{\dfrac{I_1}{P{O_1}}};{B_2} = {2.10^{ - 7}}.{\dfrac{I_2}{P{O_2}}}\) nên với B₁ = B₂ thì ta có :

\({\dfrac{I_1}{P{O_1}}} = {\dfrac{I_2}{P{O_2}}}\) hay \({\dfrac{P{O_1}}{P{O_2}}} = {\dfrac{I_1}{{I_2}}} = \dfrac{6}{9} = \dfrac{2}{3}\)

Từ đó suy ra : PO₁ = 200 mm ; PO₁ = 300 mm.

Kết luận : Trong mặt phẳng vuông góc với hai dòng điện I₁ và I₂, điểm P nằm trên đường thắng O₁O₂ với khoảng cách PO₁ = 200 mm và PO₂= 300 mm là điểm tại đó có cảm ứng từ \(\overrightarrow B = \overrightarrow 0 \)

Trong không gian, quỹ tích của điểm P là đường thẳng song song với I₁ và I₂ , cách I₁ một khoảng 200 mm và cách I₂ một khoảng 300 mm.

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài IV.10* trang 56 SBT Vật Lí 11
Giải bài IV.10* trang 56 SBT Vật Lí 11. Hai dòng điện cường độ 2,0 A và 4,0 A chạy trong hai dây dẫn thẳng dài, đồng phẳng và được đặt vuông góc với nhau trong không khí. Xác định
Bài IV.9 trang 55 SBT Vật Lí 11
Giải bài IV.9 trang 55 SBT Vật Lí 11. Ba dòng điện có cùng cường độ I1 = I2 = I3 = I và cùng chiều chạy trong ba dây dẫn thẳng dài, đồng phẳng, song song cách đều nhau.
Bài IV.8 trang 55 SBT Vật Lí 11
Giải bài IV.8 trang 55 SBT Vật Lí 11. Hai dòng điện có cường độ 4,0 A và 6,0 A chạy ngược chiều nhau trong hai dây dẫn thẳng dài song song,
Bài IV.7 trang 55 SBT Vật Lí 11
Giải bài IV.7 trang 55 SBT Vật Lí 11. Cho hai dòng điện có cùng cường độ 8 A chạy trong hai dây dẫn thẳng dài, đặt vuông góc với nhau, cách nhau một khoảng 8,0 cm trong chân không
Bài IV.6 trang 55 SBT Vật Lí 11
Giải bài IV.6 trang 55 SBT Vật Lí 11. Bắn một prôtôn với vận tốc 1,5.10^5 m/s bay vào một từ trường đều theo hướng vuông góc với các đường sức từ
Bài IV.5 trang 55 SBT Vật Lí 11
Giải bài IV.5 trang 55 SBT Vật Lí 11. Một ống dây dẫn hình trụ dài 85 cm (không lõi sắt) gồm 750 vòng dây, trong đó có dòng điện cường độ 5,6 A.
Bài IV.4 trang 55 SBT Vật Lí 11
Giải bài IV.4 trang 55 SBT Vật Lí 11. Khi cho dòng điện cường độ 10 A chạy qua một vòng dây dẫn đặt trong không khí, thì cảm ứng từ tại
Bài IV.3 trang 54 SBT Vật Lí 11
Giải bài IV.3 trang 54 SBT Vật Lí 11. Một đoạn dây dẫn dài 0,80 m đặt nghiêng một góc 600 so với hướng củ các đường sức từ trong một từ trường đều có cảm ứng từ 0,50 T.
Bài IV.2 trang 54 SBT Vật Lí 11
Giải bài IV.2 trang 54 SBT Vật Lí 11. Một đoạn dây dẫn thẳng dài 1,8 m được đặt trong một từ trường đều ccó cảm ứng từ 0,80 T. Khi có dòng điện cường độ 4,0 A chạy qua đoạn
Bài IV.1 trang 54 SBT Vật Lí 11
Giải bài IV.1 trang 54 SBT Vật Lí 11. Một đoạn dây dẫn thẳng dài 100 cm có dòng điện cường độ 20 A chạy qua và được đặt vuông góc với các đường sức từ trong một từ trường đều.