Bài 1.27 trang 20 SBT hình học 12

Giải bài 1.27 trang 20 sách bài tập hình học 12. Cho khối chóp S.ABC có thể tích bằng V. Gọi B’ và C’ lần lượt là trung điểm của SB và SC, A’ nằm trên SA sao cho . Tính thể tích khối chóp S.A’B’C’ theo V.

Đề bài

Cho khối chóp \(S.ABC\) có thể tích bằng \(V\). Gọi \(B’\) và \(C’\) lần lượt là trung điểm của \(SB\) và \(SC\), \(A’\) nằm trên \(SA\) sao cho \(\overrightarrow {SA} = 3\overrightarrow {SA'} \). Tính thể tích khối chóp \(S.A’B’C’\) theo \(V\).

Phương pháp giải - Xem chi tiết

Sử dụng công thức tính tỉ số thể tích khối chóp \(\dfrac{{{V_{S.A'B'C'}}}}{{{V_{S.ABC}}}} = \dfrac{{SA'}}{{SA}}.\dfrac{{SB'}}{{SB}}.\dfrac{{SC'}}{{SC}}\).

Lời giải chi tiết

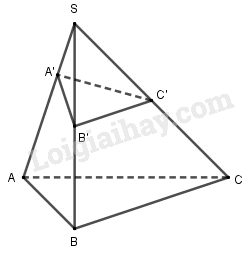
Ta có: \(\dfrac{{{V_{S.A'B'C'}}}}{{{V_{S.ABC}}}} = \dfrac{{SA'}}{{SA}}.\dfrac{{SB'}}{{SB}}.\dfrac{{SC'}}{{SC}}\)\( = \dfrac{1}{3}.\dfrac{1}{2}.\dfrac{1}{2} = \dfrac{1}{{12}}\) \( \Rightarrow {V_{S.A'B'C'}} = \dfrac{1}{{12}}{V_{S.ABC}} = \dfrac{1}{{12}}V\)

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Bài 1.26 trang 19 SBT hình học 12
Giải bài 1.26 trang 19 sách bài tập hình học 12. Cho hình hộp ABCD.A’B’C’D’ . Tính tỉ số sau...
Bài 1.25 trang 19 SBT hình học 12
Giải bài 1.25 trang 19 sách bài tập hình học 12. Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông ở B, AB = BC = AA’. Hãy chia lăng trụ đó thành ba tứ diện bằng nhau.
Bài 1.24 trang 19 SBT hình học 12
Giải bài 1.24 trang 19 sách bài tập hình học 12. Viết công thức tính thể tích hình lăng trụ, hình chóp.
Bài 1.23 trang 19 SBT hình học 12
Giải bài 1.23 trang 19 sách bài tập hình học 12. Thế nào là một hình đa diện đều. Kể tên các loại hình đa diện đều.
Bài 1.22 trang 19 SBT hình học 12
Giải bài 1.22 trang 19 sách bài tập hình học 12. Thế nào là một hình đa diện lồi. Tìm một ví dụ về một hình đa diện không lồi.
Bài 1.21 trang 19 SBT hình học 12
Giải bài 1.21 trang 19 sách bài tập hình học 12. Thế nào là hai đa diện bằng nhau. Tìm một ví dụ về hai đa diện bằng nhau.
Bài 1.20 trang 19 SBT hình học 12
Giải bài 1.20 trang 19 sách bài tập hình học 12. Tìm một ví dụ một hình tạo bởi các hình đa giác nhưng không phải là hình đa diện.
Bài 1.19 trang 19 SBT hình học 12
Giải bài 1.19 trang 19 sách bài tập hình học 12. Tìm trong thực tế một ví dụ về một hình đa diện.
Bài 1.18 trang 19 SBT hình học 12
Giải bài 1.18 trang 19 sách bài tập hình học 12. Nêu hai tính chất đặc trưng của hình đa diện.