Đề kiểm tra 45 phút (1 tiết) - Đề số 1 - Chương II - Hình học 12

Đề bài

Câu 1: Với điểm \(O\) cố định thuộc mặt phẳng \(\left( P \right)\) cho trước, xét đường thẳng \(l\) thay đổi đi qua điểm \(O\) và tạo với mặt phẳng \(\left( P \right)\) một góc \({30^o}\). Tập hợp các đường thẳng trong không gian là

A. một mặt phẳng.      B. hai đường thẳng.

C. một mặt trụ.           D. một mặt nón.

Câu 2: Diện tích xung quanh của một hình nón tròn xoay nội tiếp tứ diện đều cạnh \(a\) là

A. \({S_{xq}} = \dfrac{{\pi {a^2}}}{4}.\)          B. \({S_{xq}} = \dfrac{{\pi \sqrt 2 {a^2}}}{6}.\)

C. \({S_{xq}} = \dfrac{{\pi \sqrt 3 {a^2}}}{6}.\)    D. \({S_{xq}} = \dfrac{{2\pi {a^2}}}{3}.\)

Câu 3: Diện tích xung quanh của một hình nón tròn xoay ngoại tiếp tứ diện đều cạnh \(a\) là

A. \({S_{xq}} = \dfrac{{\pi {a^2}}}{3}.\)       B. \({S_{xq}} = \dfrac{{\pi \sqrt 2 {a^2}}}{3}.\)

C. \({S_{xq}} = \dfrac{{\pi \sqrt 3 {a^2}}}{3}.\)  D. \({S_{xq}} = \dfrac{{\pi \sqrt 3 {a^2}}}{6}.\)

Câu 4: Cho hình nón tròn xoay đỉnh \(S,\)đáy là đường tròn tâm \(O,\) bán kính đáy \(r = 5\). Một thiết diện qua đỉnh là tam giác \(SAB\) đều có cạnh bằng 8. Khoảng cách từ \(O\) đến mặt phẳng \(\left( {SAB} \right)\) bằng

A. \(\dfrac{{4\sqrt {13} }}{3}\).       B. \(\dfrac{{3\sqrt {13} }}{4}\).

C. \(3.\)                 D. \(\dfrac{{\sqrt {13} }}{3}\)

Câu 5: Cho hai điểm \(A,B\) cố định. Tập hợp các điểm \(M\) trong không gian sao cho diện tích tam giác \(MAB\) không đổi là

A. Mặt nón tròn xoay.

B. Mặt trụ tròn xoay.

C. Mặt cầu.

D. Hai đường thẳng song song

Câu 6: Cho hình trụ có bán kính đáy \(r\), đường cao \(h = OO'\). Cắt hình trụ đó bằng mặt phẳng \(\left( \alpha  \right)\) tùy ý vuông góc với đáy và cách điểm \(O\) một khoảng \(m\) cho trước (\(m < r\)). Khi ấy, mặt phẳng \(\left( \alpha  \right)\) có tính chất:

A. cắt hình trụ theo thiết diện là hình vuông.

B. luôn cách một mặt phẳng cho trước qua trục hình trụ một khoảng \(h\).

C. luôn tiếp xúc với một mặt trụ cố định.

D. cắt hình trụ theo thiết diện có diện tích \(h\left( {{r^2} - {m^2}} \right).\)

Câu 7: Một khối hộp chứ nhật nội tiếp trong một hình trụ. Ba kích thước của khối hộp chữ nhật là \(a,\,b,\,c\). Thể tích khối trụ bằng

A. \(\dfrac{{\pi \left( {{a^2} + {b^2}} \right)c}}{4}.\)

B. \(\dfrac{{\pi \left( {{c^2} + {b^2}} \right)a}}{4}.\)

C. \(\dfrac{{\pi \left( {{a^2} + {c^2}} \right)b}}{4}.\)

D.\(\dfrac{{\pi \left( {{a^2} + {b^2}} \right)c}}{4} \) hoặc \(\dfrac{{\pi \left( {{b^2} + {c^2}} \right)a}}{4}\) hoặc \(  \dfrac{{\pi \left( {{c^2} + {a^2}} \right)b}}{4}.\)

Câu 8: Một hình trụ \(\left( H \right)\) có diện tích xung quanh bằng \(4\pi \). Biết thiết diện của \(\left( H \right)\) qua trục là hình vuông. Diện tích toàn phần của \(\left( H \right)\) bằng

A. \(6\pi .\)          B. \(10\pi .\)

C. \(8\pi .\)          D. \(12\pi .\)

Câu 9: Một hình trụ có diện tích xung quanh là \(4\pi \).thiết diện qua trục là hình vuông. Một mặt phẳng \(\left( \alpha  \right)\) song song với trục, cắt hình trụ theo thiết diện \(ABB'A'\), biết một cạnh của thiết diện là một dây của đường tròn đáy của hình trụ và căng một cung \(120^\circ \). Diện tích thiết diện \(ABB'A'\) bằng

A. \(\sqrt 3 .\)        B. \(2\sqrt 3 .\)

C. \(2\sqrt 2 .\)      D. \(3\sqrt 2 .\)

Câu 10: Người ta bỏ bốn quả bóng bàn cùng kích thước, bán kính bằng \(a\) vào trong một chiếc hộp hình trụ có đáy bằng hỉnh tròn lớn của quả bóng bàn. Biết quả bóng nằm dưới cùng, quả bóng nằm trên cùng lần lượt tiếp xúc với mặt đáy dưới và mặt đáy trên của hình trụ đó. Lúc đó, diện tích xung quanh của hình trụ bằng

A. \(8\pi {a^2}.\)            B. \(4\pi {a^2}.\)

C. \(16\pi {a^2}.\)          D. \(12\pi {a^2}.\)

Câu 11: Trong số các mệnh đề sau, mệnh đề nào đúng?

A. Tồn tại duy nhất một mặt cầu đi qua hai đường tròn nằm trong hai mặt phẳng cắt nhau.

B. Tồn tại duy nhất một mặt cầu đi qua hai đường tròn nằm trong hai mặt phẳng song song.         

C. Tồn tại duy nhất một mặt cầu đi qua hai đường tròn cắt nhau.   

D. Tồn tại duy nhất một mặt cầu đi qua hai đường tròn cắt nhau nằm trong hai mặt phẳng phân biệt.

Câu 12: Cho hình trụ có bán kính đáy bằng \(3{\rm{ cm}}\), trục \(OO' = 8{\rm{ cm}}\) và mặt cầu đường kính \(OO'\). Hiệu số giữa diện tích mặt cầu và diện tích xung quanh hình trụ là

A. \(6\pi {\rm{ c}}{{\rm{m}}^2}.\) B. \(16\pi {\rm{ c}}{{\rm{m}}^2}.\)         

C. \(40\pi {\rm{ c}}{{\rm{m}}^2}.\)          D. \(208\pi {\rm{ c}}{{\rm{m}}^2}.\)

Câu 13: Thể tích của khối cầu  ngoại  tiếp một hình hộp chữ nhật có ba kích thước \(a,\,2a,\,2a\) bằng

A. \(\dfrac{{9\pi {a^3}}}{2}.\)         B. \(\dfrac{{9\pi {a^3}}}{8}.\)

C. \(\dfrac{{27\pi {a^3}}}{2}.\)       D. \(36\pi {a^3}.\)

Câu 14: Cho mặt cầu bán kính \(5{\rm{ cm}}\)và một hình trụ có bán kính đáy bằng \(3{\rm{ cm}}\) nội tiếp trong hình cầu. Thể tích của khối trụ là

A. \(24\pi {\rm{ c}}{{\rm{m}}^3}\).          B. \(36\pi {\rm{ c}}{{\rm{m}}^3}.\) 

C. \(48\pi {\rm{ c}}{{\rm{m}}^3}.\)          D. \(72\pi {\rm{ c}}{{\rm{m}}^3}.\)

Câu 15: Một mặt cầu có bán kính bằng \(10{\rm{ cm}}\). Một mặt phẳng cách tâm mặt cầu \(8{\rm{ cm}}\) cắt mặt cầu theo một đường tròn. Chu vi của đường tròn đó bằng

A. \(6\pi {\rm{ cm}}{\rm{.}}\)         B. \(12\pi {\rm{ cm}}{\rm{.}}\)

C. \(24\pi {\rm{ cm}}{\rm{.}}\)       D. \(36\pi {\rm{ cm}}{\rm{.}}\)

Câu 16: Trong các đa diện sau, đa diện nào không luôn nội tiếp được trong một mặt cầu

A. Hình chóp tam giác (tứ diện).

B. Hình chóp ngũ giác đều.

C. Hình chóp tứ giác.    

D. Hình hộp chữ nhật.

Câu 17: Cho tứ diện \(ABCD\) có \(AD \bot \left( {ABC} \right)\), \(DB \bot BC\), \(AB = AD = BC = a\). Kí hiệu \({V_1}\), \({V_2}\), \({V_3}\) lần lượt là thể tích của hình tròn xoay sinh bởi tam giác \(ABD\) khi quay quanh \(AD\), tam giác \(ABC\) khi quay quanh \(AB\), tam giác \(DBC\) khi quay quanh \(BC\). Trong các mệnh đề sau, mệnh đề nào đúng?

A. \({V_1} + {V_2} = {V_3}\).        B. \({V_1} + {V_3} = {V_2}\).

C. \({V_3} + {V_2} = {V_1}\).        D. \({V_1} = {V_2} = {V_3}\).

Câu 18: Cho các mệnh đề sau:

a. Hình chóp có đáy là hình thang thì có mặt cầu ngoại tiếp.

b. Hình chóp có đáy là hình thang cân thì có mặt cầu ngoại tiếp.

c. Hình chóp có đáy là hình chữ nhật thì có mặt cầu ngoại tiếp.

d. Hình chóp có đáy là hình thoi thì có mặt cầu ngoại tiếp.

Số mệnh đề đúng là?

A. \(0\).             B. \(1\).

C. \(2\).             D. \(3\).

Câu 19. Cho hai điểm \(A\), \(B\) phân biệt. Tập hợp tâm những mặt cầu đi qua \(A\) và \(B\) là

A. trung điểm của đoạn thẳng \(AB\).

B. mặt phẳng vuông góc với đường thẳng \(AB\).

C. mặt phẳng song song với đường thẳng \(AB\).

D. mặt phẳng trung trực của đoạn thẳng \(AB\).

Câu 20: Trong các mệnh đề sau, mệnh đề nào đúng?

A. Hình chóp có đáy là tứ giác thì có mặt cầu ngoại tiếp.

B. Hình chóp có đáy là hình thang vuông thì có mặt cầu ngoại tiếp.

C. Hình chóp có đáy là hình bình hành thì có mặt cầu ngoại tiếp.

D. Hình chóp có đáy là hình thang cân thì có mặt cầu ngoại tiếp.

Lời giải chi tiết

Câu 1:

Tập hợp các đường thẳng đó là mặt nón có góc ở đỉnh bằng \(60^0\).

Chọn D.

Câu 2:

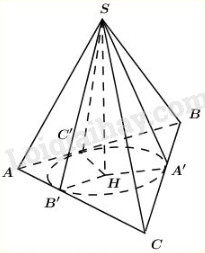
Bán kính của hình nón là: \(r = \dfrac{{a\sqrt 3 }}{2}.\dfrac{1}{3} = \dfrac{{a\sqrt 3 }}{6}\) ; đường sinh \(l = \dfrac{{a\sqrt 3 }}{2}\)

Diện tích xung quanh của hình nón là:

\({S_{xq}} = \pi rl = \pi \dfrac{{a\sqrt 3 }}{6}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{\pi {a^2}}}{4}\)

Chọn A

Câu 3:

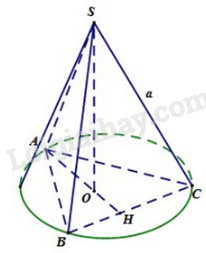
Bán kính đáy của hình nón là: \(R = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\)

Chiều cao của hình nón là: \(h = \sqrt {{a^2} - {{\left( {\dfrac{{a\sqrt 3 }}{3}} \right)}^2}}  = \dfrac{{a\sqrt 6 }}{3}\)

Diện tích xung quanh của hình nón là:

\({S_{xq}} = \pi Rl = \pi \dfrac{{a\sqrt 3 }}{3}.a = \dfrac{{\pi {a^2}\sqrt 3 }}{3}\)

Chọn A.

Câu 4:

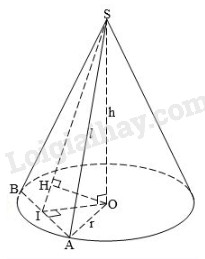
Gọi I là trung điểm của AB, H là chân đường vuông góc của O lên mp (SAB)

\(\begin{array}{l}SO = \sqrt {S{A^2} - O{A^2}}  = \sqrt {{8^2} - {5^2}}  = \sqrt {39} \\OI = \sqrt {O{A^2} - I{A^2}}  = \sqrt {{5^2} - {4^2}}  = 3\\\dfrac{1}{{O{H^2}}} = \dfrac{1}{{S{O^2}}} + \dfrac{1}{{O{I^2}}} = \dfrac{1}{{39}} + \dfrac{1}{9} = \dfrac{{16}}{{117}}\\ \Rightarrow OH = \dfrac{{3\sqrt {13} }}{4}\end{array}\)

Chọn B

Câu 5: Gọi d là khoảng cách từ điểm M đến đường thẳng AB.

Suy ra \({S_{MAB}} = \dfrac{1}{2}.d\left( {M,AB} \right).AB = \dfrac{1}{2}d.AB\)

Vì \({S_{MAB}};AB\)  là hằng số nên d không đổi .

Vậy tập hợp các điểm M thỏa mãn yêu cầu bài toán là một mặt trụ tròn xoay.

Chọn B.

Câu 8:

Gọi a là chiều cao của khối trụ suy ra khối trụ có bán kính bằng \(\dfrac{a}{2}\) .

Ta có: \({S_{xq}} = 2\pi .\dfrac{a}{2}.a = 4\pi  \Leftrightarrow a = 2\)

Diện tích toàn phần của khối trụ là: \({S_{tp}} = {S_{xq}} + 2.{S_d} = 4\pi  + 2.\pi {.1^2} = 6\pi \)

Chọn A.

Câu 9:

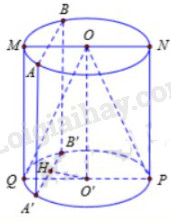
Kẻ \(O'H \bot AB \Rightarrow \sin {60^o} = \dfrac{{HB'}}{{O'B'}} = \dfrac{{\sqrt 3 }}{2} \)

\(\Rightarrow A'B' = r\sqrt 3 \)

Ta có:

\(\begin{array}{l}\left\{ \begin{array}{l}{S_{xq}} = 2\pi rh = 4\pi  \Rightarrow rh = 2\\h = MQ = QP = 2r\end{array} \right.\\ \Rightarrow A'B' = \sqrt 3\\  \Rightarrow {S_{ABB'A'}} = AA'.A'B' = 2\sqrt 3 \end{array}\)

Chọn B.

Câu 10:

Chiều cao hình trụ \(h = 4d = 4.2r = 8a\)

Bán kính đáy hình trụ là R = a

Diện tích xung quanh của khối trụ là:

\({S_{xq}} = 2\pi Rh = 2\pi .a.8a = 16\pi {a^2}\)

Chọn  C.

Câu 12: Diện tích mặt cầu có đường kính OO’ = 8 cm là:

\({S_c} = 4\pi {R^2} = 4\pi {.4^2} = 64\pi \,\left( {c{m^2}} \right)\)

Diện tích xung quanh của hình trụ là:

\({S_{xq}} = 2\pi rh = 2\pi .3.8 = 48\pi \left( {c{m^2}} \right)\)

Hiệu số giữa diện tích mặt cầu và diện tích xung quanh hình trụ là:

\(64\pi  - 48\pi  = 16\pi \left( {c{m^2}} \right)\)

Chọn B

Câu 13: Bán kính khối cầu là một nửa đường chéo của hình hộp chữ nhật \(R = \dfrac{1}{2}\sqrt {{a^2} + {{\left( {2a} \right)}^2} + {{\left( {2a} \right)}^2}}  = \dfrac{3}{2}a\)

Thể tích của khối cầu ngoại tiếp hình hộp chữ nhật là:

\(V = \dfrac{4}{3}\pi {R^3} = \dfrac{4}{3}\pi {\left( {\dfrac{3}{2}a} \right)^3} = \dfrac{9}{2}\pi {a^3}\)

Chọn A.

Câu 14:

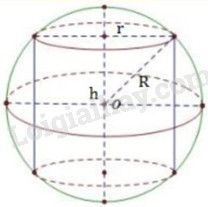
Hình trụ nội tiếp có chiều cao là:

\(h = 2.\sqrt {{5^2} - {3^2}}  = 2.4 = 8\,cm\)

Vậy thể tích khối trụ là:

\(V = \pi {r^2}h = \pi {.3^2}.8 = 72\pi \,c{m^3}\)

Chọn D.

Câu 15:

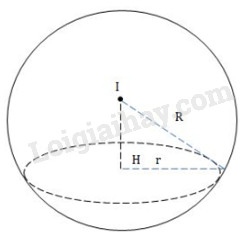
Bán kính của đường tròn đó là: \(r = \sqrt {{R^2} - O{H^2}}  = \sqrt {{{10}^2} - {8^2}}  = 6\)

Chu vi đường tròn là: \(P = 2\pi r = 2\pi .6 = 12\pi \)

Chọn B

Câu 17:

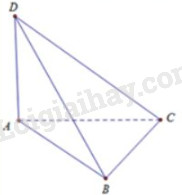
\(\left. \begin{array}{l}BC \bot AB\\BC \bot AD\end{array} \right\} \Rightarrow BC \bot AB\)  do đó tam giác ABC vuông cân tại B suy ra \(AC = a\sqrt 2 \)

Ta có:

\(\begin{array}{l}{V_1} = \dfrac{1}{3}\pi A{B^2}.AD = \dfrac{{\pi {a^3}}}{3};\\{V_2} = \dfrac{1}{3}.B{C^2}.AB = \dfrac{{\pi {a^3}}}{3}\\{V_3} = \dfrac{1}{3}\pi D{B^2}.BC\\\;\;\;\;\; = \dfrac{{\pi \left( {A{D^2} + A{B^2}} \right)}}{3}.BC = \dfrac{{2\pi {a^3}}}{3}\\ \Rightarrow {V_1} + {V_2} = {V_3}.\end{array}\)

Chọn  A.

Câu 18:

Hình chóp có đáy là hình thang cân thì có mặt cầu ngoại tiếp. (Đúng)

Hình chóp có đáy là hình chữ nhật thì có mặt cầu ngoại tiếp. (Đúng)

Chọn C

Câu 19:  Tập hợp tâm các mặt cầu đi qua hai điểm A và B là mặt phẳng trung trực của đoạn thẳng AB.

Chọn D

Loigiaihay.com