 Giải toán 10, giải bài tập Toán 10 Nâng cao, đầy đủ đại số giải tích và hình học
Giải toán 10, giải bài tập Toán 10 Nâng cao, đầy đủ đại số giải tích và hình học
 Bài 1: Bất đẳng thức và chứng minh bất đẳng thức
Bài 1: Bất đẳng thức và chứng minh bất đẳng thức
Giải bài 3 trang 109 SGK Đại số 10 nâng cao
Chứng minh rằng đẳng thức sau xảy ra với mọi các số thực a, b, c.
Đề bài
Chứng minh rằng a2 + b2 + c2 ≥ ab + bc + ca với mọi số thực a, b, c.
Đẳng thức xảy ra khi và chỉ khi a = b = c.
Lời giải chi tiết
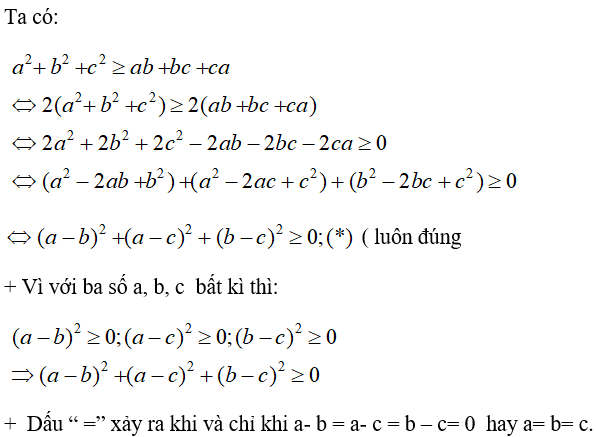
Loigiaihay.com











