Bài toán cực trị của mạch RLC mắc nối tiếp
Bài toán cực trị của mạch RLC mắc nối tiếp
CỰC TRỊ CỦA DÒNG ĐIỆN XOAY CHIỀU
I. R thay đổi
1. R THAY ĐỔI ĐỂ PMAX
a. Mạch RLC có cuộn dây thuần cảm (r=0)
\(P = UIc{\rm{os}}\varphi {\rm{ = }}{{\rm{I}}^2}R = \frac{{{U^2}}}{{{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}R = \frac{{{U^2}}}{{R + \frac{{{{\left( {{Z_L} - {Z_C}} \right)}^2}}}{R}}}\)
Để \({P_{max}} \to {\left( {R + \frac{{{{\left( {{Z_L} - {Z_C}} \right)}^2}}}{R}} \right)_{\min }}\)
Ta có: \(R + \frac{{{{\left( {{Z_L} - {Z_C}} \right)}^2}}}{R} \ge 2\sqrt {R\frac{{{{\left( {{Z_L} - {Z_C}} \right)}^2}}}{R}} = 2\left| {{Z_L} - {Z_C}} \right|\)
Dấu “=” xảy ra \( \leftrightarrow {R^2} = {({Z_L} - {Z_C})^2} \to R = \left| {{Z_L} - {Z_C}} \right|\)
b. Mạch RLC có cuộn dây không thuần cảm (r≠0)
- Công suất trên toàn mạch:
\(P{\rm{ = }}{{\rm{I}}^2}(R + r) = \frac{{{U^2}}}{{{{(R + r)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}(R + r) = \frac{{{U^2}}}{{R + r + \frac{{{{\left( {{Z_L} - {Z_C}} \right)}^2}}}{{R + r}}}}\)
Để \({P_{max}} \to {\left( {R + r + \frac{{{{\left( {{Z_L} - {Z_C}} \right)}^2}}}{{R + r}}} \right)_{\min }}\)
Ta có: \((R + r) + \frac{{{{\left( {{Z_L} - {Z_C}} \right)}^2}}}{{R + r}} \ge 2\sqrt {(R + r)\frac{{{{\left( {{Z_L} - {Z_C}} \right)}^2}}}{{R + r}}} = 2\left| {{Z_L} - {Z_C}} \right|\)
Dấu “=” xảy ra \( \leftrightarrow {(R + r)^2} = {({Z_L} - {Z_C})^2} \to R + r = \left| {{Z_L} - {Z_C}} \right| \to R = \left| {{Z_L} - {Z_C}} \right| - r\)
Chú ý: Nếu \(r > {Z_L} - {Z_C} \to {P_{{\rm{max}}}} \leftrightarrow R = 0,{P_{{\rm{max}}}} = \frac{{{U^2}}}{{{r^2} + {{({Z_L} - {Z_C})}^2}}}r\)
- Công suất trên R: \(P{\rm{ = }}\frac{{{U^2}}}{{{{(R + r)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}R = \frac{{{U^2}}}{{R + 2r + \frac{{{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}{R}}}\)
\(\begin{array}{l}A = R + 2r + \frac{{{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}{R}\\{A_{\min }} \leftrightarrow {\left( {R + \frac{{{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}{R}} \right)_{\min }}\\R + \frac{{{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}{R} \ge 2\sqrt {R.\frac{{{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}{R}} = 2\sqrt {{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \end{array}\)
Dấu “=” xảy ra: \( \leftrightarrow {R^2} = {r^2} + {\left( {{Z_L} - {Z_C}} \right)^2},{P_{{\rm{max}}}} = \frac{{{U^2}}}{{2{\rm{r}} + 2\sqrt {{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\)
- Công suất trên r: \({P_r}{\rm{ = }}\frac{{{U^2}r}}{{{{(R + r)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}\)
\({P_{r{\rm{ }}max}} = \frac{{{U^2}r}}{{{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}\) xảy ra khi R=0
2. KHI R=R1 HOẶC R=R2 THÌ P CÓ CÙNG 1 GIÁ TRỊ (P<PMAX) (CUỘN DÂY THUẦN CẢM)
\(\begin{array}{l}P = \frac{{{U^2}}}{{{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}R\\ \to P({R^2} + {\left( {{Z_L} - {Z_C}} \right)^2}) = {U^2}R\\ \leftrightarrow P{R^2} - {U^2}R + {\left( {{Z_L} - {Z_C}} \right)^2}P = 0\\ \leftrightarrow {R^2} - \frac{{{U^2}R}}{P} + {\left( {{Z_L} - {Z_C}} \right)^2} = 0{\rm{ }}(1)\end{array}\)
PT (1) có 2 nghiệm: R1, R2 : \(\left\{ \begin{array}{l}{R_1} + {R_2} = \frac{{{U^2}}}{P}\\{R_1}{R_2} = {\left( {{Z_L} - {Z_C}} \right)^2} \end{array} \right.\)
II. C thay đổi
1. C THAY ĐỔI => XẢY RA HIỆN TƯỢNG CỘNG HƯỞNG \({\varphi _{{\bf{U}}/{\bf{I}}}} = {\bf{0}}\) VÀ \({{\bf{I}}_{{\bf{MAX}}}},{\rm{ }}{{\bf{U}}_{{\bf{RMAX}}}},{\rm{ }}{{\bf{U}}_{{\bf{LMAX}}}},{\rm{ }}{{\bf{U}}_{{\bf{LCMIN}}}}\)
\({Z_L} = {Z_C}\)
Khi đó:
\(\begin{array}{l}{Z_{\min }} = R\\{I_{{\rm{max}}}} = \dfrac{U}{R}\\{P_{{\rm{max}}}} = {I^2}R = \dfrac{{{U^2}}}{R}\end{array}\)
+ Điện áp giữa hai đầu điện trở cực đại và bằng điện áp toàn mạch
\({U_L} = {U_C} \to U = \sqrt {U_R^2 + {{({U_L} - {U_C})}^2}} = {U_R}\)
+ Điện áp hai đầu đoạn mạch cùng pha với cường độ dòng điện trong mạch: φ=0
2. C THAY ĐỔI ĐỂ UCMAX VÀ ĐIỆN ÁP HAI ĐẦU ĐOẠN MẠCH VUÔNG PHA VỚI URL
Ta có: \({U_C} = I{Z_C} = \dfrac{{U{Z_C}}}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }}\)
Chia cả tử và mẫu cho ZL, ta được: \({U_C} = \dfrac{U}{{\sqrt {\dfrac{{{R^2}}}{{{Z_C}^2}} + \frac{{{{({Z_L} - {Z_C})}^2}}}{{{Z_C}^2}}} }} = \dfrac{U}{{\sqrt {\dfrac{{{R^2} + Z_L^2}}{{{Z_C}^2}} - \dfrac{{2{Z_L}}}{{{Z_C}}} + 1} }}\)
Đặt \(y = \dfrac{{{R^2} + Z_L^2}}{{{Z_C}^2}} - \dfrac{{2{Z_L}}}{{{Z_C}}} + 1 = ({R^2} + Z_L^2){x^2} - 2{Z_L}x + 1\) với $x = \dfrac{1}{{{Z_C}}}$
Ta có UCmax khi ymin
\({y_{\min }} \leftrightarrow x = - \dfrac{b}{{2{\rm{a}}}} = \dfrac{{2{Z_L}}}{{2({R^2} + Z_L^2)}} \to {Z_C} = \dfrac{{{R^2} + Z_L^2}}{{{Z_L}}}\)
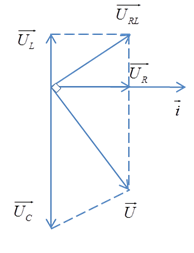
Khi đó: \({U_{Cm{\rm{ax}}}} = \dfrac{{U_R^2 + U_L^2}}{{{U_L}}} = \dfrac{{U\sqrt {{R^2} + Z_L^2} }}{R}\)
Hệ quả: \(\left\{ \begin{array}{l}{U_{RL}} \bot {U_{AB}}\\U_{C\max }^2 = {U^2} + U_{RL}^2 = {U^2} + U_R^2 + U_L^2\\U_{C\max }^{}.{U_R} = U.{U_{RL}}\\\dfrac{1}{{U_R^2}} = \dfrac{1}{{{U^2}}} + \dfrac{1}{{U_{RL}^2}}\end{array} \right.\)
3. C THAY ĐỔI ĐỂ URCMAX
Ta có: \({U_{RC}} = I{Z_{RC}} = \dfrac{{U\sqrt {{R^2} + Z_C^2} }}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }} = \dfrac{{U\sqrt {{R^2} + Z_C^2} }}{{\sqrt {{R^2} + {Z_L}^2 - 2{Z_L}{Z_C} + {Z_C}^2} }} = \dfrac{U}{{\sqrt {1 + \dfrac{{ - 2{Z_L}{Z_C} + {Z_L}^2}}{{{R^2} + Z_C^2}}} }}\)
\({U_{RLmax}} \leftrightarrow {\left( {1 + \dfrac{{ - 2{Z_L}{Z_C} + {Z_L}^2}}{{{R^2} + Z_C^2}}} \right)_{\min }}\)
\(\begin{array}{*{20}{l}}{y = 1 + \dfrac{{ - 2{Z_L}{Z_C} + {Z_L}^2}}{{{R^2} + Z_C^2}}}\\{y' = {{(1 + \dfrac{{ - 2{Z_L}{Z_C} + {Z_L}^2}}{{{R^2} + Z_C^2}})}^\prime } = \dfrac{{2{Z_C}^2 - 2{R^2} - 2{Z_L}{Z_C}}}{{{{({R^2} + Z_C^2)}^2}}}}\\{y' = 0 \leftrightarrow 2{Z_C}^2 - 2{R^2} - 2{Z_L}{Z_C} = 0}\\{\left\{ \begin{array}{l}{Z_C} > 0\\{Z_C} = \dfrac{{ - b + \sqrt \Delta }}{{2a}} = \dfrac{{{Z_L} + \sqrt {4{R^2} + Z_L^2} }}{2}\end{array} \right.}\end{array}\)
Khi đó:
\({{U}_{RC\max }}=\frac{2UR}{\sqrt{4{{R}^{2}}+Z_{L}^{2}}-{{Z}_{L}}}\)
4. C THAY ĐỔI ĐỂ URL KHÔNG PHỤ THUỘC VÀO R
URL không phụ thuộc vào R
\( \leftrightarrow {U_{RL}} = {U_{AB}}\)
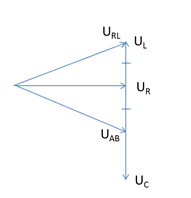
Từ giản đồ:
\(\begin{array}{l} \to {U_C} = 2{U_L}\\ \to {Z_C} = 2{Z_L}\end{array}\)
5. C THAY ĐỔI ĐỂ \({U_{RC}} \bot {U_{RL}}\)
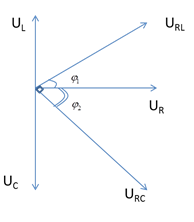
\(\begin{array}{l}{U_{RL}} \bot {U_{RC}}\\ \leftrightarrow \left\{ \begin{array}{l}\sin {\varphi _1} = c{\rm{os}}{\varphi _2}\\c{\rm{os}}{\varphi _1} = \left| {\sin {\varphi _2}} \right|\end{array} \right. \to \left| {\tan {\varphi _1}\tan {\varphi _2}} \right| = 1\\ \leftrightarrow \frac{{{U_L}}}{{{U_R}}}\frac{{{U_C}}}{{{U_R}}} = 1 \leftrightarrow {U_L}{U_C} = {U_R}^2 \leftrightarrow {Z_L}{Z_C} = {R^2}\end{array}\)
6. C=C1 HOẶC C=C2 THÌ UC CÓ CÙNG GIÁ TRỊ
\({C_1} + {C_2} = 2{C_{max}} = 2{C_0} \to {C_0} = \dfrac{{{C_1} + {C_2}}}{2}\)
7. C THAY ĐỔI CÓ 2 GIÁ TRỊ LÀM CHO: \({{\bf{I}}_{\bf{1}}} = {{\bf{I}}_{\bf{2}}},{\rm{ }}{{\bf{P}}_{\bf{1}}} = {{\bf{P}}_{\bf{2}}},{\rm{ }}{\bf{cos}}{\varphi _{\bf{1}}} = {\bf{cos}}{\varphi _{\bf{2}}},{\rm{ }}{{\bf{Z}}_{\bf{1}}} = {{\bf{Z}}_{\bf{2}}}\)
- Z1=Z2
\({R^2} + {({Z_L} - {Z_{C1}})^2} = {R^2} + {({Z_L} - {Z_{C2}})^2} \to \left| {{Z_L} - {Z_{C1}}} \right| = \left| {{Z_L} - {Z_{C2}}} \right|\)
Với ZC2>ZC1 \( \to {Z_{C1}} + {Z_{C2}} = 2{Z_L}\)
- I1=I2 hoặc P1=P2 => L=? để cộng hưởng điện
\( \leftrightarrow \left\{ \begin{array}{l}I = {I_{{\rm{max}}}}\\{\varphi _u} = {\varphi _i}\\\left| {{\rm{cos}}\varphi } \right| = 1\end{array} \right. \to 2{Z_{Cm{\rm{ax}}}} = {Z_{C1}} + {Z_{C2}}\)
III. L thay đổi
1- L THAY ĐỔI => XẢY RA HIỆN TƯỢNG CỘNG HƯỞNG \({\varphi _{{\bf{u}}/{\bf{i}}}} = {\bf{0}}\) VÀ IMAX, URMAX, UCMAX, ULCMIN
\({Z_L} = {Z_C}\)
Khi đó:
\({Z_{\min }} = R,{\rm{ }}{I_{{\rm{max}}}} = \frac{U}{R},{\rm{ }}{P_{{\rm{max}}}} = {I^2}R = \frac{{{U^2}}}{R}\)
+ Điện áp giữa hai đầu điện trở cực đại và bằng điện áp toàn mạch
\({U_L} = {U_C} \to U = \sqrt {U_R^2 + {{({U_L} - {U_C})}^2}} = {U_R}\)
+ Điện áp hai đầu đoạn mạch cùng pha với cường độ dòng điện trong mạch: φ=0I
2 - L THAY ĐỔI ĐỂ ULMAX VÀ ĐIỆN ÁP HAI ĐẦU ĐOẠN MẠCH VUÔNG PHA VỚI URC
Ta có: \({U_L} = I{Z_L} = \frac{{U{Z_L}}}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }}\)
Chia cả tử và mẫu cho ZL, ta được: \({U_L} = \frac{U}{{\sqrt {\frac{{{R^2}}}{{{Z_L}^2}} + \frac{{{{({Z_L} - {Z_C})}^2}}}{{{Z_L}^2}}} }} = \frac{U}{{\sqrt {\frac{{{R^2} + Z_C^2}}{{{Z_L}^2}} - \frac{{2{Z_C}}}{{{Z_L}}} + 1} }}\)
Đặt \(y = \frac{{{R^2} + Z_C^2}}{{{Z_L}^2}} - \frac{{2{Z_C}}}{{{Z_L}}} + 1 = ({R^2} + Z_C^2){x^2} - 2{Z_C}x + 1\) với $x = \frac{1}{{{Z_L}}}$
Ta có ULmax khi ymin
\({y_{\min }} \leftrightarrow x = - \frac{b}{{2{\rm{a}}}} = \frac{{2{Z_C}}}{{2({R^2} + Z_C^2)}} \to {Z_L} = \frac{{{R^2} + Z_C^2}}{{{Z_C}}}\)
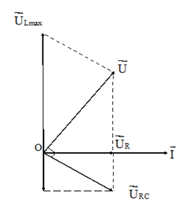
Khi đó: \({U_{Lm{\rm{ax}}}} = \frac{{U_R^2 + U_C^2}}{{{U_C}}} = \frac{{U\sqrt {{R^2} + Z_C^2} }}{R}\)
Hệ quả: \(\left\{ \begin{array}{l}{U_{RC}} \bot {U_{AB}}\\U_{L\max }^2 = {U^2} + U_{RC}^2 = {U^2} + U_R^2 + U_C^2\\U_{L\max }^{}.{U_R} = U.{U_{RC}}\\\frac{1}{{U_R^2}} = \frac{1}{{{U^2}}} + \frac{1}{{U_{RC}^2}}\end{array} \right.\)
3 - L THAY ĐỔI ĐỂ URLMAX
Ta có: \({U_{RL}} = I{Z_{RL}} = \frac{{U\sqrt {{R^2} + Z_L^2} }}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }} = \frac{{U\sqrt {{R^2} + Z_L^2} }}{{\sqrt {{R^2} + {Z_L}^2 - 2{Z_L}{Z_C} + {Z_C}^2} }} = \frac{U}{{\sqrt {1 + \frac{{ - 2{Z_L}{Z_C} + {Z_C}^2}}{{{R^2} + Z_L^2}}} }}\)
URLmax \( \leftrightarrow {\left( {1 + \frac{{ - 2{Z_L}{Z_C} + {Z_C}^2}}{{{R^2} + Z_L^2}}} \right)_{\min }}\)
\(\eqalign{& y = 1 + \frac{{ - 2{Z_L}{Z_C} + Z_C^2}}{{{R^2} + Z_L^2}} \cr & y' = \left( {1 + \frac{{ - 2{Z_L}{Z_C} + Z_C^2}}{{{R^2} + Z_L^2}}} \right)' = \frac{{2Z_L^2 - 2{R^2} - 2{Z_L}{Z_C}}}{{{{({R^2} + Z_L^2)}^2}}} \cr & y' = 0 \leftrightarrow 2Z_L^2 - 2{R^2} - 2{Z_L}{Z_C} = 0 \cr} \)
\({Z_L} > 0,{Z_L} = \frac{{ - b + \sqrt \Delta }}{{2a}} = \frac{{{Z_C} + \sqrt {4{R^2} + Z_C^2} }}{2}\)
Khi đó:
\({U_{R{L_{\max }}}} = \frac{{2UR}}{{\sqrt {4{R^2} + Z_C^2} - {Z_C}}}\)
4 - L THAY ĐỔI ĐỂ URC KHÔNG PHỤ THUỘC VÀO R
URC không phụ thuộc vào R
\( \leftrightarrow {U_{RC}} = {U_{AB}}\)
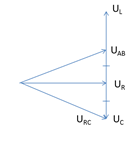
Từ giản đồ:
\(\begin{array}{l} \leftrightarrow {U_C} = {U_L} - {U_C}\\ \to {U_L} = 2{U_C}\\ \to {Z_L} = 2{Z_C}\end{array}\)
5 - L THAY ĐỔI ĐỂ \({U_{RC}} \bot {U_{RL}}\)
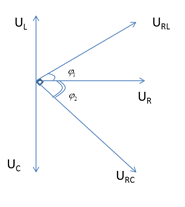
\(\begin{array}{l}{U_{RL}} \bot {U_{RC}}\\ \leftrightarrow \left\{ \begin{array}{l}\sin {\varphi _1} = c{\rm{os}}{\varphi _2}\\c{\rm{os}}{\varphi _1} = \left| {\sin {\varphi _2}} \right|\end{array} \right. \to \left| {\tan {\varphi _1}\tan {\varphi _2}} \right| = 1\\ \leftrightarrow \frac{{{U_L}}}{{{U_R}}}\frac{{{U_C}}}{{{U_R}}} = 1 \leftrightarrow {U_L}{U_C} = {U_R}^2 \leftrightarrow {Z_L}{Z_C} = {R^2}\end{array}\)
6 - L=L1HOẶC L=L2 THÌ UL CÓ CÙNG GIÁ TRỊ
\(\frac{1}{{{L_{{\rm{max}}}}}} = \frac{1}{2}(\frac{1}{{{L_1}}} + \frac{1}{{{L_2}}})\)
7 - L THAY ĐỔI, CÓ 2 GIÁ TRỊ CỦA L LÀM CHO \({{\bf{I}}_{\bf{1}}} = {{\bf{I}}_{\bf{2}}},{\rm{ }}{{\bf{P}}_{\bf{1}}} = {{\bf{P}}_{\bf{2}}},{\rm{ }}{\bf{cos}}{\varphi _{\bf{1}}} = {\bf{cos}}{\varphi _{\bf{2}}},{\rm{ }}{{\bf{Z}}_{\bf{1}}} = {{\bf{Z}}_{\bf{2}}}\)
- Z1=Z2
\({R^2} + {({Z_{L1}} - {Z_C})^2} = {R^2} + {({Z_{L2}} - {Z_C})^2} \to \left| {{Z_{L1}} - {Z_C}} \right| = \left| {{Z_{L2}} - {Z_C}} \right|\)
Với ZL2>ZL1 \( \to {Z_{L1}} + {Z_{L2}} = 2{Z_C}\)
- I1=I2 hoặc P1=P2 => L=? để cộng hưởng điện
\( \leftrightarrow \left\{ \begin{array}{l}I = {I_{{\rm{max}}}}\\{\varphi _u} = {\varphi _i}\\\left| {{\rm{cos}}\varphi } \right| = 1\end{array} \right. \to L = \frac{{{L_1} + {L_2}}}{2}\)
IV. \(\omega\) thay đổi
1. \(\omega \) THAY ĐỔI ĐỂ XẢY RA HIỆN TƯỢNG CỘNG HƯỞNG ĐIỆN: \({Z_{min}},{\rm{ }}{I_{max}},{\rm{ }}{U_{Rmax}},{\rm{ }}{P_{ABmax}},{\rm{ }}cos\varphi \) CỰC ĐẠI
\({Z_L} = {Z_C} \to {\omega ^2} = \frac{1}{{LC}}{\rm{ hay }}\omega = \frac{1}{{\sqrt {LC} }}\)
Khi đó:
\({Z_{\min }} = R,{\rm{ }}{I_{{\rm{max}}}} = \dfrac{U}{R},{\rm{ }}{P_{{\rm{max}}}} = {I^2}R = \dfrac{{{U^2}}}{R}\)
+ Điện áp giữa hai đầu điện trở cực đại và bằng điện áp toàn mạch
\({U_L} = {U_C} \to U = \sqrt {U_R^2 + {{({U_L} - {U_C})}^2}} = {U_R}\)
+ Điện áp hai đầu đoạn mạch cùng pha với cường độ dòng điện trong mạch: \(\varphi = 0\)
2. \(\omega \) THAY ĐỔI ĐỂ UCMAX
\({U_C} = I{Z_C} = \dfrac{{U{Z_C}}}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }} = \dfrac{U}{{\omega C\sqrt {{R^2} + {\omega ^2}{L^2} - 2\dfrac{L}{C} + \dfrac{1}{{{\omega ^2}{C^2}}}} }} = \dfrac{U}{{C\sqrt {{\omega ^4}{L^2} + ({R^2} - 2\dfrac{L}{C}){\omega ^2} + \dfrac{1}{{{C^2}}}} }}\)
UC max <=> mẫu min
Đặt \({\omega ^2} = x\) , \( \to {x^2}{L^2} + ({R^2} - 2\dfrac{L}{C})x + \dfrac{1}{{{C^2}}} = y\)
\({y_{\min }} \leftrightarrow x = - \dfrac{b}{{2{\rm{a}}}} = \dfrac{1}{{LC}} - \dfrac{{{R^2}}}{{2{L^2}}},{y_{\min }} = - \dfrac{\Delta }{{4{\rm{a}}}} = \dfrac{{{R^2}}}{{LC}} - \dfrac{{{R^4}}}{{2{L^2}}}\)
Khi đó ta có:
\(\begin{array}{l}{Z_L} = \omega L = \sqrt {\dfrac{1}{{LC}} - \dfrac{{{R^2}}}{{2{L^2}}}} L \to Z_L^2 = \dfrac{L}{C} - \dfrac{{{R^2}}}{2}\\ \leftrightarrow Z_L^2 = {Z_L}{Z_C} - \dfrac{{{R^2}}}{2}\\ \to \dfrac{{{R^2}}}{2} = {Z_L}\left( {{Z_C} - {Z_L}} \right)\\ \to \dfrac{{{Z_L}}}{R}\dfrac{{\left( {{Z_C} - {Z_L}} \right)}}{R} = \dfrac{1}{2} \leftrightarrow \tan {\varphi _{RL}}\tan \varphi = -\dfrac{1}{2}\end{array}\)
Vẽ giản đồ ta được:
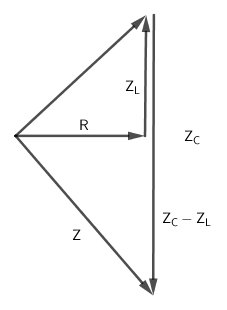
Từ giản đồ, ta có:
\(\begin{array}{l}{Z^2} = {R^2} + {\left( {{Z_C} - {Z_L}} \right)^2} = 2{Z_L}\left( {{Z_C} - {Z_L}} \right) + {\left( {{Z_C} - {Z_L}} \right)^2}\\ \leftrightarrow {Z^2} = Z_C^2 - Z_L^2\end{array}\)
Kết luận: \(\omega \) biên thiên để \({U_{{C_{max}}}}\), khi đó:
\({U_{Cm{\rm{ax}}}} = \dfrac{{2UL}}{{R\sqrt {4LC - {R^2}{C^2}} }},{\rm{ }}{\omega ^2}{\rm{ = }}\dfrac{1}{{LC}} - \dfrac{{{R^2}}}{{2{L^2}}}\)
\(\tan {\varphi _{RL}}\tan \varphi = -\dfrac{1}{2}\) và \(Z_C^2 = {Z^2} + Z_L^2\)
3. \(\omega \) THAY ĐỔI ĐỂ ULMAX
\({U_L} = I{Z_L} = \dfrac{{U{Z_L}}}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }} = \dfrac{{U\omega L}}{{\sqrt {{R^2} + {\omega ^2}{L^2} - 2\dfrac{L}{C} + \dfrac{1}{{{\omega ^2}{C^2}}}} }} = \dfrac{{UL}}{{\sqrt {{L^2} + \dfrac{{({R^2} - 2\dfrac{L}{C})}}{{{\omega ^2}}} + \dfrac{1}{{{\omega ^4}{C^2}}}} }}\)
\({U_{L{\rm{ }}max}}\) <=> mẫu min
Đặt \(\dfrac{1}{{{\omega ^2}}} = x\), \( \to {L^2} + ({R^2} - 2\dfrac{L}{C})x + {x^2}\dfrac{1}{{{C^2}}} = y\)
\({y_{\min }} \leftrightarrow x = - \dfrac{b}{{2{\rm{a}}}} = \dfrac{{2LC - {R^2}{C^2}}}{2},{y_{\min }} = - \dfrac{\Delta }{{4{\rm{a}}}} = \dfrac{{4L{{\rm{R}}^2} - {R^4}C}}{4}C\)
Khi đó ta có:
\(\begin{array}{l} \to Z_C^2 = \dfrac{1}{{{\omega ^2}{C^2}}} = \dfrac{1}{{\dfrac{2}{{2LC - {R^2}{C^2}}}{C^2}}} = \dfrac{L}{C} - \dfrac{{{R^2}}}{2}\\ \leftrightarrow Z_C^2 = {Z_L}{Z_C} - \dfrac{{{R^2}}}{2}\\ \leftrightarrow \dfrac{{{R^2}}}{2} = {Z_C}\left( {{Z_L} - {Z_C}} \right) \leftrightarrow \dfrac{{{Z_C}}}{R}\dfrac{{\left( {{Z_L} - {Z_C}} \right)}}{R} = \dfrac{1}{2}\\ \leftrightarrow \tan {\varphi _{RC}}\tan \varphi = -\dfrac{1}{2}\end{array}\)
Vẽ giản đồ ta được:
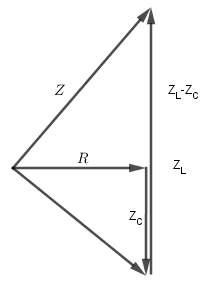
Từ giản đồ, ta có:
\(\begin{array}{l}{Z^2} = {R^2} + {\left( {{Z_L} - {Z_C}} \right)^2} = 2{Z_C}\left( {{Z_L} - {Z_C}} \right) + {\left( {{Z_C} - {Z_L}} \right)^2}\\ \leftrightarrow {Z^2} = Z_L^2 - Z_C^2\end{array}\)
Kết luận: \({U_{Lm{\rm{ax}}}} = \dfrac{{2UL}}{{R\sqrt {4LC - {R^2}{C^2}} }},{\rm{ }}{\omega ^2}{\rm{ = }}\dfrac{2}{{2LC - {R^2}{C^2}}}\)
\(\tan {\varphi _{RC}}\tan \varphi =- \dfrac{1}{2}\) và \(Z_L^2 = {Z^2} + Z_C^2\)
Khi \(\omega \) thay đổi để \({U_{Cmax}},{\rm{ }}{U_{Lmax}}\)
\(\begin{array}{l}{U_{Cm{\rm{ax}}}} = {U_{Lm{\rm{ax}}}} = \dfrac{{2UL}}{{R\sqrt {4LC - {R^2}{C^2}} }}\\{\omega _L}.{\omega _C} = \dfrac{1}{{LC}} = \omega _0^2\end{array}\)
4. THAY ĐỔI \(f\) CÓ HAI GIÁ TRỊ \({f_{\bf{1}}} \ne {f_{\bf{2}}}\) BIẾT \({f_{\bf{1}}} + {f_{\bf{2}}} = {\rm{ }}{\bf{a}}\) VÀ CÙNG CÔNG SUẤT HOẶC CÙNG \({\bf{I}},{\bf{Z}},{\bf{cos}}\varphi ,{{\bf{U}}_{{\bf{R}}.}}\)
- Hai giá trị tần số làm cho mạch có cùng công suất nên:
\(\begin{array}{l}{P_1} = {P_2} \Leftrightarrow I_1^2R = I_2^2R \Leftrightarrow I_1^2 = I_2^2\\ \to \dfrac{{{U^2}}}{{{R^2} + {{({Z_{L1}} - {Z_{C1}})}^2}}} = \dfrac{{{U^2}}}{{{R^2} + {{({Z_{L2}} - {Z_{C2}})}^2}}}\\ \to {({Z_{L1}} - {Z_{C1}})^2} = {({Z_{L2}} - {Z_{C2}})^2} \to \left[ \begin{array}{l}{Z_{L1}} - {Z_{C1}} = {Z_{L2}} - {Z_{C2}}(loai)\\{Z_{L1}} - {Z_{C1}} = - ({Z_{L2}} - {Z_{C2}})\end{array} \right.\\ \to {Z_{L1}} + {Z_{L2}} = {Z_{C1}} + {Z_{C2}}) \to L({\omega _1} + {\omega _2}) = \dfrac{1}{C}(\dfrac{1}{{{\omega _1}}} + \dfrac{1}{{{\omega _2}}}) = \dfrac{1}{C}\dfrac{{{\omega _1} + {\omega _2}}}{{{\omega _1}{\omega _2}}}\\ \to {\omega _1}{\omega _2} = \dfrac{1}{{LC}} = \omega _0^2\end{array}\)
- Công thức trên áp dụng cho bài toán thay đổi f có cùng I, Z, cosφ, UR
Các hệ quả thu được:
- Cảm kháng và dung kháng trong hai trường hợp:
\({({Z_{L1}} - {Z_{C1}})^2} = {({Z_{L2}} - {Z_{C2}})^2}{\rm{ hay }}\left| {{Z_L} - {Z_C}} \right| = h/s \to \left| \begin{array}{l}{Z_{L1}} = {Z_{C2}}\\{Z_{L2}} = {Z_{C1}}\end{array} \right.\)
- Hệ số công suất trong hai trường hợp: \({\rm{cos}}{\varphi _1} = {\rm{cos}}{\varphi _2} = \dfrac{1}{{\sqrt {1 + k{{(\sqrt {\dfrac{{{\omega _1}}}{{{\omega _2}}}} - \sqrt {\dfrac{{{\omega _2}}}{{{\omega _1}}}} )}^2}} }}{\rm{ (}}\dfrac{L}{C} = k.{R^2})\)
- Cường độ dòng điện trong hai trường hợp: \({I_1} = {I_2} = \dfrac{{{I_{{\rm{max}}}}}}{n}\)
Điện trở của mạch được xác định: \(R = L\dfrac{{\left| {{\omega _1} - {\omega _2}} \right|}}{{\sqrt {{n^2} - 1} }} = \dfrac{{\left| {{\omega _1} - {\omega _2}} \right|}}{{{\omega _1}{\omega _2}C\sqrt {{n^2} - 1} }}\)
Các bài khác cùng chuyên mục
- Phương pháp giải bài tập phân hạch - nhiệt hạch
- Phương pháp giải bài tập về phóng xạ
- Phương pháp giải bài tâp phản ứng hạt nhân
- Phương pháp giải bài tập của chuyển động electron quang điện trong điện trường đều và từ trường đều
- Phương pháp giải bài tập về cường độ dòng quang điện bão hòa và hiệu suất lượng tử
- Phương pháp giải bài tập phân hạch - nhiệt hạch
- Phương pháp giải bài tập về phóng xạ
- Phương pháp giải bài tâp phản ứng hạt nhân
- Phương pháp giải bài tập của chuyển động electron quang điện trong điện trường đều và từ trường đều
- Phương pháp giải bài tập về cường độ dòng quang điện bão hòa và hiệu suất lượng tử













Danh sách bình luận