-
GIẢI TÍCH - TOÁN 12 NÂNG CAO
-
CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
- Bài 1. Tính đơn điệu của hàm số
- Bài 2. Cực trị của hàm số
- Bài 3. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
- Bài 4. Đồ thị của hàm số và phép tịnh tiến hệ tọa độ
- Bài 5. Đường tiệm cận của đồ thị hàm số
- Bài 6. Khảo sát sự biến thiên và vẽ đồ thị của một hàm số đa thức
- Bài 7: Khảo sát sự biến thiên và vẽ đồ thị hàm số của một số hàm phân thức hữu tỉ
- Bài 8. Một số bài toán thường gặp về đồ thị
- Câu hỏi và bài tập chương I - Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
- Bài tập trắc nghiệm khách quan chương I - Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số - Toán 12 Nâng cao
-
CHƯƠNG II. HÀM SỐ LŨY THỪA, HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
- Bài 1. Lũy thừa với số mũ hữu tỉ
- Bài 2. Lũy thừa với số mũ thực
- Bài 3. Lôgarit
- Bài 4. Số e và loogarit tự nhiên
- Bài 5. Hàm số mũ và hàm số lôgarit
- Bài 6. Hàm số lũy thừa
- Bài 7. Phương trình mũ và lôgarit
- Bài 8. Hệ phương trình mũ và lôgarit
- Bài 9. Bất phương trình mũ và lôgarit
- Ôn tập chương II - Hàm số lũy thừa, hàm số mũ và hàm số lôgarit
- Bài tập trắc nghiệm khách quan chương II - Hàm số lũy thừa, hàm số mũ và hàm số lôgarit - Toán 12 Nâng cao
-
CHƯƠNG III. NGUYÊN HÀM, TÍCH PHÂN VÀ ỨNG DỤNG
- Bài 1. Nguyên hàm
- Bài 2. Một số phương pháp tìm nguyên hàm
- Bài 3. Tích phân
- Bài 4. Một số phương pháp tích phân
- Bài 5. Ứng dụng tích phân để tính diện tích hình phẳng
- Bài 6. Ứng dụng tích phân để tính thể tích vật thể
- Ôn tập chương III - Nguyên hàm, tích phân và ứng dụng
- Bài tập trắc nghiệm khách quan chương III - Nguyên hàm, tích phân và ứng dụng - Toán 12 Nâng cao
-
CHƯƠNG IV. SỐ PHỨC
-
ÔN TẬP CUỐI NĂM ĐẠI SỐ VÀ GIẢI TÍCH - TOÁN 12 NÂNG CAO
-
-
HÌNH HỌC - TOÁN 12 NÂNG CAO
Giải bài tập Toán 12 Nâng cao, Toán 12 Nâng cao, đầy đủ giải tích và hình học
Câu hỏi và bài tập chương I - Ứng dụng đạo hàm để khảo ..
Bài 72 trang 62 SGK giải tích 12 nâng cao
Cho hàm số: a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho. b) Chứng minh rằng phương trình f(x) =0 có ba nghiệm phân biệt.
Cho hàm số: \(f\left( x \right) = {1 \over 3}{x^3} - 2{x^2} + {{17} \over 3}\)
LG a
Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho.
Lời giải chi tiết:
TXĐ: \(D =\mathbb R\)
\(\eqalign{
& \mathop {\lim }\limits_{x \to + \infty } y = + \infty ;\,\mathop {\lim }\limits_{x \to - \infty } y = - \infty \cr
& f'\left( x \right) = {x^2} - 4x\cr&f'\left( x \right) = 0 \Leftrightarrow {x^2} - 4x = 0 \Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr
x = 4 \hfill \cr} \right.\cr&f\left( 0 \right) = {{17} \over 3};\,f\left( 4 \right) = - 5 \cr} \)
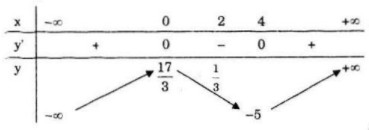
Hàm số đồng biến trên các khoảng (-∞,0) và (4; +∞)
Hàm số nghịch biến trên khoảng (0; 4)
Hàm số đạt cực đại tại x = 0; yCĐ=y(0)=17/3
Hàm số đạt cực tiểu tại x = 4, yCT=y(4)=-5
\(\eqalign{
& f''\left( x \right) = 2x - 4\cr&f''\left( x \right) = 0 \Leftrightarrow x = 2 \cr
& f\left( 2 \right) = {1 \over 3} \cr} \)
Điểm uốn \(I\left( {2;{1 \over 3}} \right)\)
Đồ thị nhận I làm tâm đối xứng.
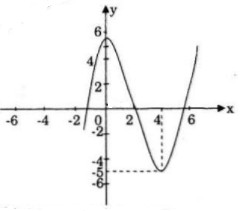
Đồ thị:
LG b
Chứng minh rằng phương trình f(x) =0 có ba nghiệm phân biệt.
Lời giải chi tiết:
Quan sát đồ thị ta thấy, đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt nên phương trình f(x) =0 có ba nghiệm phân biệt.
Cách khác:
Hàm số đã cho có giá trị cực đại và giá trị cực tiểu trái dấu, tức hai điểm cực đại và cực tiểu của đồ thị nằm về hai phía đối với trục hoành do đó đồ thị hàm số cắt trục hoành tại ba điểm phân biệt nên phương trình f(x) =0 có ba nghiệm phân biệt.
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 73 trang 62 SGK giải tích 12 nâng cao
- Bài 74 trang 62 SGK giải tích 12 nâng cao
- Bài 75 trang 62 SGK giải tích 12 nâng cao
- Bài 76 trang 62 SGK giải tích 12 nâng cao
- Bài 77 trang 62 SGK giải tích 12 nâng cao
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
