 Giải bài tập Toán 12 Nâng cao, Toán 12 Nâng cao, đầy đủ giải tích và hình học
Giải bài tập Toán 12 Nâng cao, Toán 12 Nâng cao, đầy đủ giải tích và hình học
 Câu hỏi và bài tập chương I - Ứng dụng đạo hàm để khảo ..
Câu hỏi và bài tập chương I - Ứng dụng đạo hàm để khảo ..
Bài 69 trang 61 SGK giải tích 12 nâng cao
Xét chiều biến thiên và tìm cực trị (nếu có) của các hàm số sau:
Xét chiều biến thiên và tìm cực trị (nếu có) của các hàm số sau:
LG a
\(y = \sqrt {3x + 1} \)
Lời giải chi tiết:
TXĐ: \(D = \left[ { - {1 \over 3}; + \infty } \right)\)
\(y' = {3 \over {2\sqrt {3x + 1} }} > 0\,\forall x > - {1 \over 3}\)
Hàm số đồng biến \(\left( { - {1 \over 3}; + \infty } \right)\), hàm số không có cực trị.
LG b
\(y = \sqrt {4x - {x^2}} \)
Lời giải chi tiết:
ĐK: \(4x - {x^2} \ge 0 \Leftrightarrow 0 \le x \le 4\)
TXĐ: \(D = \left[ {0;4} \right]\)
\(y' = {{4 - 2x} \over {2\sqrt {4x - {x^2}} }}\), \(\forall x \in \left( {0;4} \right)\)
\(y' = 0 \Leftrightarrow x = 2;\,y\left( 2 \right) = 2\)
Bảng biến thiên
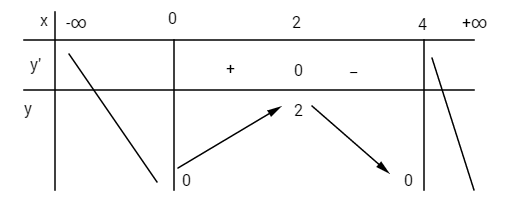
Hàm số đạt cực đại tại điểm \(x = 2\); giá trị cực đại \(y(2) = 2\).
LG c
\(y = x + \sqrt x \)
Lời giải chi tiết:
TXĐ: \(D = \left[ {0; + \infty } \right)\)
\(y' = 1 + {1 \over {2\sqrt x }} > 0,\,\forall x > 0\)
Hàm số đồng biến trên khoảng \(\left( {0; + \infty } \right)\), hàm số không có cực trị.
LG d
\(y = x - \sqrt x \)
Lời giải chi tiết:
TXĐ: \(D = \left[ {0; + \infty } \right)\)
\( y' = 1 - {1 \over {2\sqrt x }} \), \(\forall x \in \left( {0; + \infty } \right)\)
\(y' = 0 \)\( \Leftrightarrow 1 - \frac{1}{{2\sqrt x }} = 0\)
\( \Leftrightarrow \frac{{2\sqrt x - 1}}{{2\sqrt x }} = 0 \Leftrightarrow 2\sqrt x - 1 = 0\) \( \Leftrightarrow \sqrt x = \frac{1}{2} \Leftrightarrow x = \frac{1}{4}\)
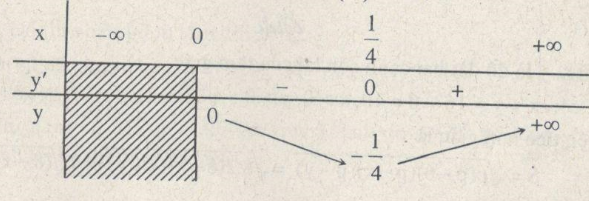
Hàm số đạt cực tiểu tại điểm \(x = {1 \over 4}\); giá trị cực tiểu \(y\left( {{1 \over 4}} \right) = - {1 \over 4}\)
Loigiaihay.com












Danh sách bình luận