Bài 70 trang 61 SGK giải tích 12 nâng cao

Người ta định làm một cái hộp hình trụ bằng tôn có thể tích V cho trước. Tìm bán kính đáy r và chiều cao của hình trụ sao cho tốn ít nguyên liệu nhất.

Đề bài

Người ta định làm một cái hộp hình trụ bằng tôn có thể tích \(V\) cho trước. Tìm bán kính đáy \(r\) và chiều cao của hình trụ sao cho tốn ít nguyên liệu nhất.

Lời giải chi tiết

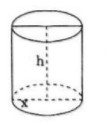
Thể tích của hình trụ là: \(V = B.h = \pi {r^2}.h \Rightarrow h = {V \over {\pi {r^2}}}\)

Diện tích toàn phần của hình trụ là:

\(S = 2\pi {r^2} + 2\pi r.h = 2\pi {r^2} + 2\pi .r.{V \over {\pi {r^2}}} \) \(= 2\pi {r^2} + {{2V} \over r}\)

Xét hàm số:

\(\eqalign{
& S\left( r \right) = 2\pi {r^2} + {{2V} \over r}\,\,\left( {r > 0} \right) \cr
& S' = 4\pi r - {{2V} \over {{r^2}}} = {{4\pi {r^3} - 2V} \over {{r^2}}} \cr
& S' = 0 \Leftrightarrow 4\pi {r^3} - 2V = 0\cr& \Leftrightarrow {r^3} = \frac{V}{{2\pi }} \Leftrightarrow r = \root 3 \of {{V \over {2\pi }}} \cr} \)

Bảng biến thiên:

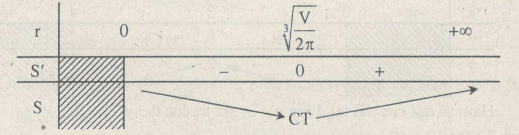
\(S\) đạt giá trị nhỏ nhất tại điểm \(r = \root 3 \of {{V \over {2\pi }}} \) khi đó \(h = {V \over {\pi {r^2}}} = {V \over {\pi \root 3 \of {{{{V^2}} \over {4{\pi ^2}}}} }} = \root 3 \of {{{4V} \over \pi }} \)

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.1 trên 7 phiếu

Bài tiếp theo

Bài 71 trang 62 SGK giải tích 12 nâng cao
Chu vi của một tam giác là 16cm, độ dài một cạnh tam giác là 6cm. Tìm độ dài hai cạnh còn lại của tam giác sao cho tam giác có diện tích lớn nhât.
Bài 72 trang 62 SGK giải tích 12 nâng cao
Cho hàm số: a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho. b) Chứng minh rằng phương trình f(x) =0 có ba nghiệm phân biệt.
Bài 73 trang 62 SGK giải tích 12 nâng cao
Cho hàm số a) Tìm điều kiện đối với p và q để hàm số f có một cực đại và một cực tiểu. b) Chứng minh rằng nếu giá trị cực đại và giá trị cực tiểu trái dấu thì phương trình: có ba nghiệm phân biệt. c) Chứng minh rằng điều kiện cần và đủ để phương trình (1) có ba nghiệm phân biệt là:
Bài 74 trang 62 SGK giải tích 12 nâng cao
Cho hàm số: a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số. b) Viết phương trình tiếp tuyến của đồ thị tại điểm uốn U của nó. c) Gọi là đường thẳng đi qua điểm U và có hệ số góc m. Tìm các giá trị của m sao cho đường thẳng cắt đồ thị của hàm số đã cho tại ba điểm phân biệt.
Bài 75 trang 62 SGK giải tích 12 nâng cao
Cho hàm số: a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số với m = 2. b) Tìm các giá trị của m sao cho đồ thị của hàm số cắt trục hoành tại bốn điểm, tạo thành ba đoạn thẳng có độ dài bằng nhau.
Bài 76 trang 62 SGK giải tích 12 nâng cao
Cho hàm số a) Khảo sát sự biến thiên và vẽ đồ thị hàm số đã cho. b) Từ đồ thị của hàm số y = f(x) suy ra cách vẽ đồ thị của hàm số
Bài 77 trang 62 SGK giải tích 12 nâng cao
Cho hàm số: a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số với m =1. b) Chứng minh rằng với mọi , các đường cong đều đi qua hai điểm cố định A và B.
Bài 78 trang 62 SGK giải tích 12 nâng cao
a) Vẽ đồ thị (P) của hàm số và đồ thị (H) của hàm số . b) Tìm giao điểm của hai đường cong (P) và (H). Chứng minh rằng hia đường cong đó có tiếp tuyến chung tại giao điểm của chúng. c) Xác định các khoảng trên đó (P) nằm phía trên hoặc phía dưới (H).
Bài 79 trang 62 SGK giải tích 12 nâng cao
Cho hàm số : a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số. b) Tiếp tuyến của đường cong (C) tại điểm cắt tiệm cận đứng và tiệm cận xiên tại hai điểm A và B. Chứng minh rằng M là trung điểm của đoạn thẳng AB và tam giác OAB có diện tích không phụ thuộc vào vị trí điểm M trên đường cong (C).
Bài 69 trang 61 SGK giải tích 12 nâng cao
Xét chiều biến thiên và tìm cực trị (nếu có) của các hàm số sau:
Bài 68 trang 61 SGK giải tích 12 nâng cao
Chứng minh các bất đẳng thức sau: