-
ĐẠI SỐ - SBT TOÁN 10 NÂNG CAO
-
Chương 1: Mệnh đề - Tập hợp
-
Chương 2: Hàm số
-
CHƯƠNG III. PHƯƠNG TRÌNH BẬC NHẤT VÀ BẬC HAI
- Bài 1. Đại cương về phương trình
- Bài 2. Phương trình bậc nhất và bậc hai một ẩn
- Bài 3. Một số phương trình quy về phương trình bậc nhất hoặc bậc hai
- Bài 4. Phương trình và hệ phương trình bậc nhất nhiều ẩn
- Bài 5. Một số ví dụ về hệ phương trình bậc hai hai ẩn
- Bài tập Ôn tập chương III - Phương trình bậc nhất và bậc hai
-
CHƯƠNG IV. BẤT ĐẲNG THỨC VÀ BẤT PHƯƠNG TRÌNH
- Bài 1. Bất đẳng thức và chứng minh bất đẳng thức
- Bài 2. Đại cương về bất phương trình
- Bài 3. Bất phương trình và hệ bất phương trình bậc nhất một ẩn
- Bài 4. Dấu của nhị thức bậc nhất
- Bài 5. Bất phương trình và hệ bất phương trình bậc nhất hai ẩn
- Bài 6. Dấu của tam thức bậc hai
- Bài 7. Bất phương trình bậc hai
- Bài 8. Một số phương trình và bất phương trình quy về bậc hai
- Bài tập Ôn tập chương IV - Bất đẳng thức và bất phương trình
-
CHƯƠNG V. THỐNG KÊ
-
CHƯƠNG VI. GÓC LƯỢNG GIÁC VÀ CÔNG THỨC LƯỢNG GIÁC
-
BÀI TẬP ÔN TẬP CUỐI NĂM - ĐẠI SỐ 10 NÂNG CAO
-
-
HÌNH HỌC-SBT TOÁN 10 NÂNG CAO
Bài 56 trang 109 SBT Hình học 10 Nâng cao
Giải bài tập Bài 56 trang 109 SBT Hình học 10 Nâng cao
Cho hai đường tròn
\(({C_1}): {x^2} + {y^2} - 4x - 8y + 11 = 0 ; \)
\( ({C_1}): {x^2} + {y^2} - 2x - 2y - 2 = 0\).
LG a
Xét vị trí tương đối của \((C_1)\) và \((C_2)\).
Lời giải chi tiết:
\((C_1)\) có tâm \(I_1(2 ; 4)\), bán kính \({R_1} = \sqrt {{2^2} + {4^2} - 11} = 3\).
\((C_2)\) có tâm \(I_2(1 ; 1)\), bán kính \({R_2} = \sqrt {{1^2} + {1^2} + 2} = 2\).
\(1 = |{R_1} - {R_2}| < {I_1}{I_2}\)
\(= \sqrt {{{(1 - 2)}^2} + {{(1 - 4)}^2}}\)
\( = \sqrt {10} < {R_1} + {R_2} = 5\).
Suy ra \((C_1)\) và \((C_2)\) cắt nhau.
LG b
Viết phương trình tiếp tuyến chung của \((C_1)\) và \((C_2).\)
Lời giải chi tiết:
(h.107).
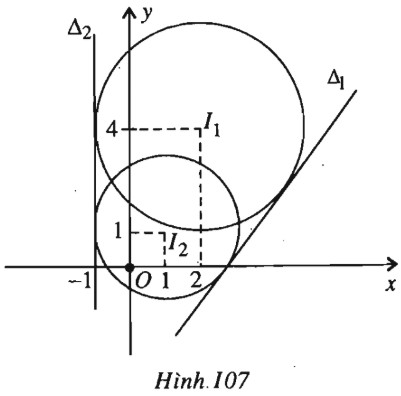
Theo câu a), \((C_1)\) và \((C_2)\) cắt nhau nên chúng có hai tiếp tuyến chung. Tiếp tuyến chung \(\Delta \) có phương trình : \(\alpha x + \beta y + \gamma = 0 ({\alpha ^2} + {\beta ^2} > 0)\).
\(\Delta \) tiếp xúc với \((C_1)\) và \((C_2)\) khi và chỉ khi \(\left\{ \begin{array}{l}d({I_1} ; \Delta ) = {R_1}\\d({I_2} ; \Delta ) = {R_2}\end{array} \right.\)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l} \dfrac{{|2\alpha + 4\beta + \gamma |}}{{\sqrt {{\alpha ^2} + {\beta ^2}} }} = 3 (1)\\ \dfrac{{|\alpha + \beta + \gamma |}}{{\sqrt {{\alpha ^2} + {\beta ^2}} }} = 2 (2)\end{array} \right.\\ \Rightarrow 2|2\alpha + 4\beta + \gamma | = 3|\alpha + \beta + \gamma |\\ \Leftrightarrow 4\alpha + 8\beta + 2\gamma = \pm (3\alpha + 3\beta + 3\gamma )\\ \Leftrightarrow \left[ \begin{array}{l}\gamma = \alpha + 5\beta \\\gamma = - \dfrac{{7\alpha + 11\beta }}{5}.\end{array} \right.\end{array}\)
Thay \(\gamma = \alpha + 5\beta \) vào (2) ta có:
\( \dfrac{{|2\alpha + 6\beta |}}{{\sqrt {{\alpha ^2} + {\beta ^2}} }} = 2\)
\( \Leftrightarrow {(\alpha + 3\beta )^2} = {a^2} + {\beta ^2} \)
\( \Leftrightarrow 2\beta (4\beta + 3\alpha ) = 0\)
\( \Leftrightarrow \beta = 0\) hoặc \(4\beta = - 3\alpha \).
Với \(\beta = 0\)( do đó \(\alpha \ne 0\)), suy ra \(\gamma = \alpha \). Ta có tiếp tuyến chung thứ nhất
\({\Delta _1}: x + 1 = 0\).
Với \(4\beta = - 3\alpha \), chọn \(\alpha = 4, \beta = - 3\), ta được \(\gamma = - 11\). Ta có tiếp tuyến chung thứ hai
\({\Delta _2}: 4x - 3y - 11 = 0\).
Thay \(\gamma = - \dfrac{{7\alpha + 11\beta }}{5}\) vào (2), ta có
\( \dfrac{{|2\alpha + 6\beta |}}{{5\sqrt {{\alpha ^2} + {\beta ^2}} }} = 2 \)
\( \Leftrightarrow {(\alpha + 3\beta )^2} = 25({\alpha ^2} + {\beta ^2})\)
\( \Leftrightarrow 12{\alpha ^2} - 3\alpha \beta + 8{\beta ^2} = 0\), phương trìn vô nghiệm.
Vậy \((C_1)\) và \((C_2)\) có hai tiếp tuyến chung là
\(\begin{array}{l}{\Delta _1}: x + 1 = 0;\\{\Delta _2}: 4x - 3y - 11 = 0.\end{array}\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 57 trang 109 SBT Hình học 10 Nâng cao
- Bài 58 trang 109 SBT Hình học 10 Nâng cao
- Bài 55 trang 108 SBT Hình học 10 Nâng cao
- Bài 54 trang 108 SBT Hình học 10 Nâng cao
- Bài 53 trang 108 SBT Hình học 10 Nâng cao
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
