Giải toán 10, giải bài tập Toán 10 Nâng cao, đầy đủ đại số giải tích và hình học Ôn tập chương I - Vectơ - Toán 10 Nâng cao

Bài 4 trang 34 SGK Hình học 10 Nâng cao


Cho tam giác ABC.

Lựa chọn câu để xem lời giải nhanh hơn

Cho tam giác \(ABC\).

LG a

Tìm các điểm \(M\) và \(N\) sao cho

\(\overrightarrow {MA}  - \overrightarrow {MB}  + \overrightarrow {MC}  = \overrightarrow 0 \) và \(2\overrightarrow {NA}  + \overrightarrow {NB}  + \overrightarrow {NC}  = \overrightarrow 0 .\)

Lời giải chi tiết:

 

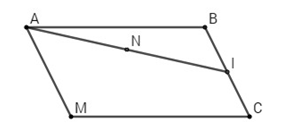
Ta có \(\overrightarrow {MA}  - \overrightarrow {MB}  + \overrightarrow {MC}  = \overrightarrow 0 \)

\(\Leftrightarrow \,\overrightarrow {BA}  + \overrightarrow {MC}  = \overrightarrow 0 \)

\(\begin{array}{l}
\Leftrightarrow \overrightarrow {BA} = - \overrightarrow {MC} \\
\Leftrightarrow \overrightarrow {BA} = \overrightarrow {CM}
\end{array}\)

Do đó \(ABCM\) là hình bình hành.

Gọi \(I\) là trung điểm của \(BC\), ta có \(\overrightarrow {NB}  + \overrightarrow {NC}  = 2\overrightarrow {NI} \) suy ra \(2\overrightarrow {NA}  + 2\overrightarrow {NI}  = \overrightarrow 0 \)

\( \Rightarrow \,\,\overrightarrow {NA}  + \overrightarrow {NI}  = \overrightarrow 0 \)

\(\Rightarrow \,N\,\) là trung điểm của \(AI\).

LG b

Với các điểm \(M, N\) ở câu a) , tìm các số \(p\) và \(q\) sao cho

\(\overrightarrow {MN}  = p\overrightarrow {AB}  + q\overrightarrow {AC} .\)

Phương pháp giải:

- Biểu diễn \(\overrightarrow {AM} ,\,\overrightarrow {AN} \) qua \(\overrightarrow {AB} ,\,\overrightarrow {AC} \).

- Từ đó suy ra véc tơ MN.

Lời giải chi tiết:

Từ câu a), ta biểu diễn \(\overrightarrow {AM} ,\,\overrightarrow {AN} \) qua \(\overrightarrow {AB} ,\,\overrightarrow {AC} \).

Do ABCM là hình bình hành nên:

\(\overrightarrow {AM}  = \overrightarrow {BC}  = \overrightarrow {AC}  - \overrightarrow {AB} \)

Do N là trung điểm AI nên:

\(\begin{array}{l}
\overrightarrow {AN} = \frac{1}{2}\overrightarrow {AI} = \frac{1}{2}.\frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\\
= \frac{1}{4}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) = \frac{1}{4}\overrightarrow {AB} + \frac{1}{4}\overrightarrow {AC}
\end{array}\)

(vì I là trung điểm BC nên \(\overrightarrow {AI}  = \frac{1}{2}\left( {\overrightarrow {AB}  + \overrightarrow {AC} } \right)\))

Do đó,

\(\begin{array}{l}
\overrightarrow {MN} = \overrightarrow {AN} - \overrightarrow {AM} \\
= \frac{1}{4}\overrightarrow {AB} + \frac{1}{4}\overrightarrow {AC} - \overrightarrow {AC} + \overrightarrow {AB} \\
= \frac{5}{4}\overrightarrow {AB} - \frac{3}{4}\overrightarrow {AC} \\
\Rightarrow \overrightarrow {MN} = \frac{5}{4}\overrightarrow {AB} - \frac{3}{4}\overrightarrow {AC}
\end{array}\)

Vậy \(p = {5 \over 4}\,;\,q =  - {3 \over 4}.\)

Loigiaihay.com


Bình chọn:
3.5 trên 12 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Hãy viết chi tiết giúp Loigiaihay.com

Vui lòng để lại thông tin để ad có thể liên hệ với em nhé!

Vấn đề em gặp phải là gì ?

Hãy viết chi tiết giúp Loigiaihay.com

Cảm ơn bạn đã sử dụng Loigiaihay.com. Đội ngũ giáo viên cần cải thiện điều gì để bạn cho bài viết này 5* vậy?

Vui lòng để lại thông tin để ad có thể liên hệ với em nhé!

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store