Giải toán 10, giải bài tập Toán 10 Nâng cao, đầy đủ đại số giải tích và hình học Ôn tập chương I - Vectơ - Toán 10 Nâng cao

Bài 11 trang 36 SGK Hình học 10 Nâng cao


Cho tam giác đều ABC có cạnh bằng a.

Đề bài

Cho tam giác đều \(ABC\) có cạnh bằng \(a\). Giá trị \(\left| {\overrightarrow {AB}  - \overrightarrow {CA} } \right|\) bằng bao nhiêu ?

(A) \(2a\) ;                              (B) \(a\);

(C) \(a\sqrt 3 \);                            (D) \({{a\sqrt 3 } \over 2}\).

Lời giải chi tiết

 

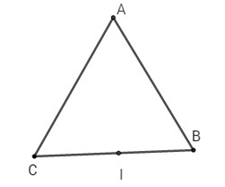
Gọi \(I\) là trung điểm \(BC\).

Ta có \(\overrightarrow {AB}  - \overrightarrow {CA}  = \overrightarrow {AB}  + \overrightarrow {AC}  = 2\overrightarrow {AI} \).

\( \Rightarrow \,\,\left| {\overrightarrow {AB}  - \overrightarrow {CA} } \right| = 2\left| {\overrightarrow {AI} } \right|\)

Mà \(AI = \sqrt {A{B^2} - B{I^2}}  \)\(= \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}}  = \frac{{a\sqrt 3 }}{2}\)

Nên \(\left| {\overrightarrow {AB}  - \overrightarrow {CA} } \right| = 2AI = 2.\frac{{a\sqrt 3 }}{2} = a\sqrt 3 \)

Chọn (C).

Loigiaihay.com


Bình chọn:
3.7 trên 3 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store