Giải bài tập vật lý 12, Vật lý 12 - Để học tốt vật lý 12 Bài 36. Năng lượng liên kết của hạt nhân. Phản ứng hạt ..

Lý thuyết năng lượng liên kết của hạt nhân, phản ứng hạt nhân


1. Lực tương tác giữa các nuclôn gọi là lực hạt nhân (tương tác hạt nhân hay tương tác mạnh).

Lực tương tác giữa các nuclon gọi là lực hạt nhân (tương tác hạt nhân hay tương tác mạnh)

Lực hạt nhân chỉ phát huy tác dụng trong phạm vi kích thước hạt nhân (khoảng 10-15 m)

1. ĐỘ HỤT KHỐI

\(\Delta m = Z{m_p} + \left( {A - Z} \right){m_n} - {m_X}\)

(Khối lượng của một hạt nhân luôn nhỏ hơn tổng khối lượng của các nuclôn tạo thành hạt nhân đó)

2. NĂNG LƯỢNG LIÊN KẾT

Năng lượng liên kết của một hạt nhân là năng lượng tối thiểu cần thiết phải cung cấp để tách các nuclon; nó được tính bằng tích của độ hụt khối của hạt nhân với thừa số c2.

\({{\rm{W}}_{lk}} = \left[ {Z{m_p} + \left( {A - Z} \right){m_n} - {m_X}} \right]{c^2} = \Delta m{c^2}\)

Các hạt nhân bền vững có \(\dfrac{{{{\rm{W}}_{lk}}}}{A}\) lớn nhất vào cỡ 8,8 MeV/nuclon; đó là những hạt nhân nằm khoảng giữa của bảng tuần hoàn ứng với 50 < A < 80

3. NĂNG LƯỢNG LIÊN KẾT RIÊNG

Mức độ bền vững của một hạt nhân tùy thuộc vào năng lượng liên kết riêng

\(\varepsilon  = \dfrac{{{{\rm{W}}_{lk}}}}{A}\)

4. PHẢN ỨNG HẠT NHÂN

Phản ứng hạt nhân là quá trình biến đổi của các hạt nhân, được chia thành hai loại:

- Phản ứng hạt nhân tự phát

- Phản ứng hạt nhân kích thích

5. CÁC ĐỊNH LUẬT BẢO TOÀN

\(A + B \to C + D\)

1. Bảo toàn điện tích

\({Z_A} + {\rm{ }}{Z_B} = {\rm{ }}{Z_C} + {\rm{ }}{Z_D}\)

2. Bảo toàn số nuclon (bảo toàn số A)

\({A_A} + {\rm{ }}{A_B} = {\rm{ }}{A_C} + {\rm{ }}{A_D}\)

3. Bảo toàn năng lượng toàn phần

\({W_t} = {\rm{ }}{W_s}\)

4. Bảo toàn động lượng

\(\overrightarrow {{P_t}}  = \overrightarrow {{P_s}} \)

-Không có định luật bảo toàn khối lượng

\(\Delta {m_A} + \Delta {m_B} \ne \Delta {m_C} + \Delta {m_D}\) (vì \({{\rm{W}}_{l{k_A}}} + {{\rm{W}}_{l{k_B}}} \ne {{\rm{W}}_{l{k_C}}} + {{\rm{W}}_{l{k_D}}}\) )

- Không có định luật bảo toàn số proton

6. NĂNG LƯỢNG CỦA MỘT PHẢN ỨNG HẠT NHÂN

- Năng lượng của phản ứng hạt nhân

\(\begin{array}{l}\Delta E = \left( {\sum {m{}_{trc} - \sum {{m_{sau}}} } } \right){c^2} = \left( {\sum {{{\rm{W}}_{{{\rm{d}}_{{\rm{s}}au}}}} - \sum {{{\rm{W}}_{{d_{trc}}}}} } } \right)\\ = \left( {\sum {\Delta {m_{sau}} - \sum {\Delta {m_{trc}}} } } \right){c^2} = \sum {{{\left( {{{\rm{W}}_{lk}}} \right)}_{sau}} - \sum {{{\left( {{{\rm{W}}_{lk}}} \right)}_{trc}}} } \end{array}\)

 Nếu:

  • \(\Delta E{\rm{ }} > {\rm{ }}0\) : thì tỏa nhiệt
  • \(\Delta E{\rm{ }} < {\rm{ }}0\): thì thu nhiệt

Nếu phản ứng hạt nhân tỏa năng lượng thì năng lượng tỏa ra dưới dạng động năng của các hạt sản phẩm và năng lượng photon γ. Năng lượng tỏa ra đó thường được gọi là năng lượng hạt nhân.

Năng lượng do 1 phản ứng hạt nhân tỏa ra là:

\(\Delta E = \left( {\sum {m{}_{trc} - \sum {{m_{sau}}} } } \right){c^2} > 0\)

Năng lượng do N phản ứng là: \[Q{\rm{ }} = {\rm{ }}N\Delta E\]

Nếu cứ 1 phản ứng có k hạt thì số phản ứng : \(N = \frac{1}{k}{N_X} = \frac{1}{k}\frac{{{m_X}}}{{{A_X}}}{N_A}\)

*** Photon tham gia phản ứng:

Giả sử hạt nhân A đứng yên hấp thụ photon gây ra phản ứng hạt nhân:

\(\gamma  + A \to B + C\)

Áp dụng định luật bảo toàn năng lượng toàn phần:

\(\varepsilon  + {m_A}{c^2} = \left( {{m_B} + {m_C}} \right){c^2} + \left( {{{\rm{W}}_B} + {{\rm{W}}_C}} \right)\) với \(\varepsilon  = hf = \frac{{hc}}{\lambda }\)

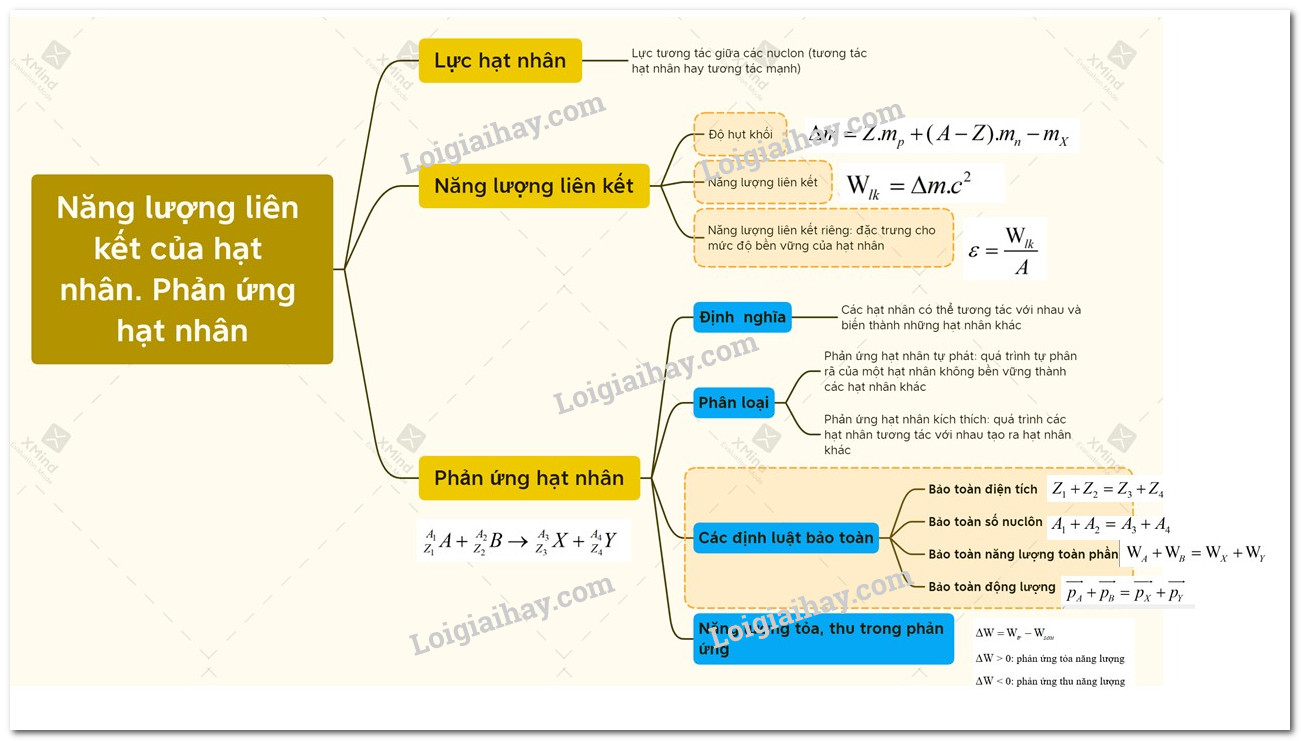
Sơ đồ tư duy về năng lượng liên kết của hạt nhân. Phản ứng hạt nhân



Bình chọn:
3.6 trên 5 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Lí lớp 12 - Xem ngay

Báo lỗi - Góp ý

Group Ôn Thi ĐGNL & ĐGTD Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store