Giải SBT toán hình học và đại số 10 nâng cao Bài 1 + 2. Góc và cung lượng giác. Giá trị lượng giác c..

Câu 6.4 trang 195 SBT Đại số 10 Nâng cao


Giải bài tập Câu 6.4 trang 195 SBT Đại số 10 Nâng cao

Đề bài

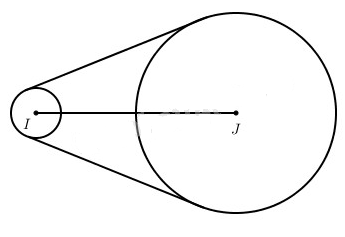
Một dây curoa quân quanh hai trục tròn tâm I bán kính 1dm và tâm J bán kính 5dm mà khoảng cách IJ là 8dm (h.6.1). Hãy tính độ dài của dây cu-roa.

Lời giải chi tiết

Gọi A, B là hai điểm tiếp xúc của dây curoa theo thứ tự với đường tròn tâm I và tâm J (A, B nằm cùng phía đối với đường thẳng IJ). Ta có \(\cos \widehat {BJI} = \dfrac{{R - r}}{d} = \dfrac{{5 - 1}}{8} = \dfrac{1}{2}\) (r = 1 là bán kính của đường tròn tâm I, R = 5dm là bán kính của đường tròn tâm J, \(d = IJ = 8dm\) là khoảng cách giữa hai tâm). Vậy \(\widehat {BJI} = \alpha  = \dfrac{\pi }{3}\) .

Dễ thấy chiều dai dây curoa bằng:

\(\begin{array}{l}2\left[ {R\left( {\pi  - \alpha } \right) + r\alpha  + d\sin \alpha } \right] = 2\left( {\dfrac{{11\pi }}{3} + 4\sqrt 3 } \right)\\ \approx 36,89\left( {dm} \right)\end{array}\)

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store