Giải vở bài tập Toán lớp 4 tập 1, tập 2 Chương 6 : Ôn tập

Bài 172 : Luyện tập chung


Giải bài tập 1, 2, 3, 4, 5 trang 111, 112, 113 VBT toán 4 bài 172 : Luyện tập chung với lời giải chi tiết và cách giải nhanh, ngắn nhất

Lựa chọn câu để xem lời giải nhanh hơn

Bài 1

Số dân của 4 tỉnh (theo số liệu năm 2011) được cho trong bảng sau :

Tỉnh

Hà Giang

Quảng Bình

Nình Thuận

Cà Mau

Số dân

746 300

853 000

569 000

1 214 900

Tên các tỉnh có số dân Từ ít đến nhiều (trong bảng trên) là……………..

Phương pháp giải:

So sánh số dân của các tỉnh rồi sắp xếp các tỉnh có số dân theo thứ tự từ ít đến nhiều.

Lời giải chi tiết:

Ta có : 569 000  <  746 300  <  853 000  <  1 214 900.

Vậy tên các tỉnh có số dân từ ít đến nhiều là: Ninh Thuận; Hà Giang ; Quảng Bình ; Cà Mau.

Bài 2

Tính: 

a) \(\displaystyle \frac{4}{7} + \frac{5}{{14}} - \frac{1}{2}\)

b) \(\displaystyle \frac{9}{{17}} + \frac{9}{{34}} \times \frac{2}{3} \)

c)\(\displaystyle \frac{5}{9} \times \frac{3}{{10}}:\frac{7}{{12}} \)

Phương pháp giải:

- Biểu thức có các phép tính cộng, trừ, nhân, chia thì ta thực hiện tính phép nhân, chia trước, thực hiện phép cộng, trừ sau.

- Biểu thức chỉ có phép cộng và phép trừ hoặc chỉ có phép nhân và phép chia thì ta thực hiện lần lượt từ trái sang phải.

Lời giải chi tiết:

a) \(\displaystyle \frac{4}{7} + \frac{5}{{14}} - \frac{1}{2} = \frac{{8 }}{{14}}  + \frac{5}{{14}}- \frac{1}{2}\)\(\displaystyle = \frac{{13}}{{14}} - \frac{1}{2} = \frac{{13 }}{{14}} - \frac{7}{14}= \frac{6}{{14}} = \frac{3}{7}\)

b) \(\displaystyle \frac{9}{{17}} + \frac{9}{{34}} \times \frac{2}{3} = \frac{9}{{17}} + \frac{{9 \times 2}}{{34 \times 3}}\)\(\displaystyle = \frac{9}{{17}} + \frac{3}{{17}} = \frac{{9 + 3}}{{17}} = \frac{{12}}{{17}}\) 

c) \(\displaystyle \frac{5}{9} \times \frac{3}{{10}}:\frac{7}{{12}} = \frac{{5 \times 3}}{{9 \times 10}}:\frac{7}{{12}}\)\(\displaystyle = \frac{1}{6} \times \frac{{12}}{7} = \frac{{1 \times 12}}{{6 \times 7}} = \frac{2}{7}\)

Bài 3

Tìm \(\displaystyle x\) : 

a) \(\displaystyle x - \frac{5}{6} = \frac{2}{3}\)                                          b) \(\displaystyle x:\frac{2}{5} = 10\)

Phương pháp giải:

Áp dụng các quy tắc:

- Muốn tìm số bị trừ ta lấy hiệu cộng với số trừ.

- Muốn tìm số bị chia ta lấy thương nhân với số chia.

Lời giải chi tiết:

\(\displaystyle \begin{array}{l}a) \;x - \dfrac{5}{6} = \dfrac{2}{3}\\ \;\;\;\;x = \dfrac{2}{3} + \dfrac{5}{6} \\ \;\;\;\;x = \dfrac{{9}}{6}=\dfrac{3}{2}\end{array}\)

\(\displaystyle \begin{array}{l}b)\;x:\dfrac{2}{5} = 10\\ \;\;\;\;x{\rm{ }} = {\rm{ }}10 \times \dfrac{2}{5}\\ \;\;\;\;x = 4\end{array}\) 

Bài 4

 Tìm ba số tự nhiên liên tiếp biết tổng của ba số đó là 198.

Phương pháp giải:

Vì ba số đó là ba số tự nhiên liên tiếp nên hai số liền nhau hơn hoặc kém nhau 1 đơn vị.

Vẽ sơ đồ biểu thị ba số, sau đó dựa vào sơ đồ tìm số thứ nhất, sau đó lần lượt tìm hai số còn lại. 

Lời giải chi tiết:

Vì ba số đó là ba số tự nhiên liên tiếp nên hai số liền nhau hơn hoặc kém nhau 1 đơn vị.

Ta có sơ đồ :

Ba lần số thứ nhất bằng:

            \(198 - (1 + 1 + 1) = 195\)

Số thứ nhất là:

            \(195 : 3 = 65\)

Số thứ hai là:

             \(65 + 1 = 66\)

Số thứ ba là:

             \( 66 + 1 = 67\)

Vậy ba số tự nhiên liên tiếp có tổng bằng \(198\) lần lượt là \( 65\,; \;66\,;\; 67\).

Lưu ý : Cũng có thể giải như sau :

Nhận xét : Trung bình cộng của ba số tự nhiên liên tiếp chính là số ở giữa ba số đó, hay chính là số thứ hai.

Số thứ hai là : 

             \(198 : 3 = 66\)

Số thứ nhất là:

             \(66 -1 = 65\)

Số thứ ba là:

             \( 66 + 1 = 67\)

Vậy ba số tự nhiên liên tiếp có tổng bằng \(198\) lần lượt là \( 65\,; \;66\,;\; 67\).

Bài 5

Một lớp học có 33 học sinh, trong đó có số học sinh trai bằng \(\dfrac{4}{7}\) số học sinh gái. Hỏi lớp học đó có bao nhiêu học sinh trai?


Phương pháp giải:

1. Vẽ sơ đồ: coi số học sinh trai gồm 4 phần bằng nhau thì số học sinh gái gồm 7 phần như thế.

2. Tìm tổng số phần bằng nhau.

3. Tìm giá trị của 1 phần bằng cách lấy tổng hai số chia cho tổng số phần bằng nhau.

4. Tìm số học sinh trai (lấy giá trị một phần nhân với số phần biểu diễn số học sinh trai).

Chú ý: Bước 3 và bước 4 có thể gộp lại thành một bước.

Lời giải chi tiết:

Ta có sơ đồ : 

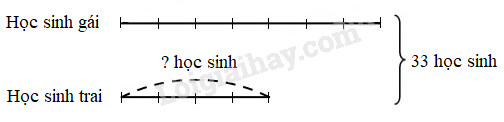
Theo sơ đồ, tổng số phần bằng nhau là :

7 + 4 = 11 (phần)

Lớp học đó có số học sinh trai là:

 33 : 11 × 4 = 12 (học sinh)

Đáp số : 12 học sinh.

Loigiaihay.com


Bình chọn:
4.6 trên 121 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán lớp 4 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K15 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store