Bài 102 : Luyện tập
Giải bài tập 1, 2, 3, 4, 5 trang 21 VBT toán 4 bài 102 : Luyện tập với lời giải chi tiết và cách giải nhanh, ngắn nhất
Bài 1
Rút gọn các phân số :
\(\displaystyle\eqalign{
& {{21} \over 28} = \;...\,\,\,\,\,\,\,\,\,\,\quad \quad \quad \quad \quad \quad {9 \over {36}} =\; ... \cr
& {{18} \over {54}} =\; ...\,\,\,\,\,\,\,\,\,\,\quad \quad \quad \quad \quad \quad{{30} \over {48}} =\; ... \cr
& {{90} \over {72}} =\; ...\,\,\,\,\,\,\,\,\,\,\quad \quad \quad \quad \quad \quad{{72} \over {42}} =\; ... \cr} \)
Phương pháp giải:
Cách rút gọn phân số:
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn một
- Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản (phân số không thể rút gọn được nữa).
Lời giải chi tiết:
\(\displaystyle {{21} \over 28} = \dfrac{21:7}{28:7}= {3 \over 4}\) \(\displaystyle{9 \over {36}}=\dfrac{9:9}{36 : 9} = {1 \over 4}\)
\(\dfrac{18}{54}= \dfrac{18:18}{54:18}= \dfrac{1}{3}\) \(\displaystyle{{30} \over {48}} = \dfrac{30 : 6}{48 : 6}= {5 \over 8} \)
\(\displaystyle {{90} \over {72}}= \dfrac{90:18}{72:18} = {5 \over 4}\) \(\displaystyle{{72} \over {42}} = \dfrac{72:6}{42:6}= {{12} \over 7} \)
Bài 2
Khoanh vào những phân số bằng \(\displaystyle{3 \over 4}\) :
\(\displaystyle{9 \over {12}}\,\,\,\,\,;\,\,\,\,{{15} \over {16}}\,\,\,\,\,;\,\,\,\,\,{{15} \over {20}}\,\,\,\,;\,\,\,\,\,{{18} \over {25}}\,\,\,\,;\,\,\,\,{{18} \over {24}}\)
Phương pháp giải:
Rút gọn các phân số thành phân số tối giản (nếu được). Các phân số bằng phân số \(\displaystyle{3 \over 4}\) thì rút gọn được thành phân số tối giản là \(\displaystyle{3 \over 4}\).
Lời giải chi tiết:
\(\dfrac{9}{12}=\dfrac{ 9: 3}{ 12: 3}=\dfrac{3}{4}\) ; \(\dfrac{15}{20}=\dfrac{15 :5 }{20 :5 }=\dfrac{3}{4}\) ;
\(\dfrac{18}{24}=\dfrac{18 : 6}{24 :6 }=\dfrac{3}{4}\) ;
\(\dfrac{15}{16}\) và \(\dfrac{18}{25}\) là phân số tối giản.
Vậy ta có kết quả như sau :
Bài 3
Khoanh vào những phân số bằng \(\displaystyle{{25} \over {100}}\) :
\(\displaystyle{5 \over {20}}\,\,\,\,;\,\,\,\,{{15} \over {65}}\,\,\,\,;\,\,\,\,{3 \over {12}}\,\,\,\,;\,\,\,\,{8 \over 2}\,\,\,\,;\,\,\,\,{{20} \over {80}}\)
Phương pháp giải:
Rút gọn các phân số thành phân số tối giản (nếu được). Các phân số cùng phân số tối giản thì bằng nhau.
Lời giải chi tiết:
\(\dfrac{25}{100}=\dfrac{ 25: 25}{ 100: 25}=\dfrac{1}{4}\) ; \(\dfrac{5}{20}=\dfrac{5 : 5}{20 : 5}=\dfrac{1}{4}\) ;
\(\dfrac{15}{65}=\dfrac{15 :5 }{65 :5 }=\dfrac{3}{13}\) ; \(\dfrac{3}{12}=\dfrac{3 :3 }{12 :3 }=\dfrac{1}{4}\) ;
\(\dfrac{8}{2}=\dfrac{ 8:2 }{2 :2 }=\dfrac{4}{1}=4\) ; \(\dfrac{20}{80}=\dfrac{ 20:20 }{80 : 20}=\dfrac{1}{4}\).
Vậy ta có kết quả như sau :
Bài 4
Tính theo mẫu:
Mẫu: \(\dfrac{ \not{4}\times 7 \times \not{9}}{\not{4}\times 5 \times \not{9}} = \dfrac{7} {5}\)
a) \(\displaystyle{{2 \times 5 \times 11} \over {3 \times 11 \times 5}} = ....\)
b) \(\displaystyle{{8 \times 12 \times 17} \over {19 \times 12 \times 8}} = ...\)
c) \(\displaystyle{{6 \times 9 \times 11} \over {11 \times 9 \times 12}} = .....\)
Phương pháp giải:
Cùng chia nhẩm tích ở trên và tích ở dưới gạch ngang cho các thừa số chung.
Lời giải chi tiết:
a) \(\displaystyle{{2 \times \not{5} \times \not{11}} \over {3 \times \not{11} \times \not{5}}} = \dfrac{2}{3}\)
b) \(\displaystyle{{\not{8} \times \not{12} \times 17} \over {19 \times \not{12} \times \not{8}}} = \dfrac{17}{19}\)
c) \(\displaystyle{{6 \times \not{9} \times \not{11}} \over {\not{11} \times \not{9} \times 12}} = \dfrac{6}{12}=\dfrac{1}{2}\)
Bài 5
Đúng ghi Đ, sai ghi S :
a) \(\dfrac{6\times \not{2} + \not{4}}{7\times \not{2} + \not{4}} =\dfrac{6}{7}\)
b) \(\dfrac{6\times 2 + 4}{7\times 2 + 4} = \dfrac{16}{18} = \dfrac{8}{9}\)
Phương pháp giải:
Tính giá trị biểu thức ở tử số và mẫu số, sau đó rút gọn phân số thu được thành phân số tối giản.
Lời giải chi tiết:
Ta có : \(\dfrac{6\times 2 + 4}{7\times 2 + 4} =\dfrac{12+4}{14+4} = \dfrac{16}{18} = \dfrac{8}{9}\).
Vậy ta có kết quả :
a) \(\dfrac{6\times \not{2} + \not{4}}{7\times \not{2} + \not{4}} =\dfrac{6}{7}\) S
b) \(\dfrac{6\times 2 + 4}{7\times 2 + 4} = \dfrac{16}{18} = \dfrac{8}{9}\) Đ
Loigiaihay.com
Các bài khác cùng chuyên mục





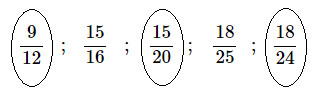
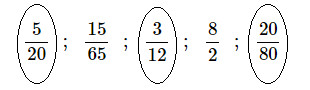







Danh sách bình luận